|
Fundamental Quantum Cosmological Units and the Quantum Evolution of the Universeby Louis Nielsen, Senior Physics MasterE-mail: INTERNET:
louis44nielsen@gmail.com
Introduction
In the following I shall show that in our Universe there is an absolute and
cosmological system of units independent of living creatures and specific local systems.
In my Holistic Quantum Cosmology I have based the theoretical deductions on the
existence of a physically smallest distance – elementary length – and a
physically smallest time interval – elementary time – together with the
total matter/energy mass of the Universe. You can read a summary, or
the full text, or go to the main index with
entry points to all parts of the treatise.
My discovery of a connection between the total mass of the Universe, elementary
length, elementary time, Planck's Constant and the light constant gives a holistic
context of our Universe. There is a connection between microcosmos and macrocosmos. As
the smallest physical distance is determined by the total mass of the Universe, it can
be expressed: "The Greatest is contained in the Smallest!" In my Holistic Quantum Cosmology I have shown which connection there is between
the actual extent of the Universe, its age (the cosmic time parameter), elementary
length and elementary time. Likewise I have shown the connection between the total
mass of the Universe and the smallest possible mass – elementary mass. The Universe has developed from one quantum – the cosmic embryoton.
This cosmic embryoton had an extension equal to elementary length, and the Universe
– space, time, and thereby the nature laws – were formed within the first
cosmic quantum interval. The evolution of the Universe is guided by a cosmic
evolution quantum number "ticking" up through the natural numbers.
The Universe was "born" when this number was one (unity)! "Today"
this cosmic quantum number is extremely high, 7.2 · 10127. The evolution of the Universe is characterized by the original cosmic embryoton
being split up in more and more elementary quanta. The actual number of these
elementary quanta is equal to the cosmic evolution quantum number. The division and spreading of the energy originally concentrated in the cosmic
embryoton is in accordance with the entropy law, "demanding" that a system
evolves from a less probable and dense state to a more probable and less dense state. As the Universe develops from one single quantum mass to more and more quantum masses,
spreading in the expanding space, a consequence will be that the cosmic unit for mass
will vary as the Universe evolves! This cosmic variation of the physical basic unit for
mass has very interesting consequences for the physical quantities we have defined in
order to describe the Universe, of which we are ourselves a part. As it will be shown
in the following, the evolution of the Universe can be characterized by a development
up through the natural numbers! Given in cosmological units, many of the physical
quantities we presume constant will vary . This is f.i. the case with Planck's
"constant".
Physical Quantities and their Units
In order to describe the phenomena in the Universe, of which we are part ourselves,
we have defined physical quantities. A physical quantity is characterized by a
mathematical number, a unit and maybe a direction.Our apparent feeling, that we live in a Universe controlled by certain laws, is a.o.
caused by the discovery that between certain physical quantities there exists a
mathematical connection, often even a simple one. Experience has shown that all physical quantities can be defined by a few
fundamental physical quantities. Even if we have more possibilities to choose
physical fundamental quantities, it looks like the Universe "itself" has
decided which basic quantities shall be used when deducting other physical quantities.
These fundamental quantities are: - Distance in space between two "points",
- Time interval between two events, and
- Mass of a matter/energy containing system.
In order to be able to indicate definite distances, time intervals and masses it is
necessary – also for communication of these quantities to others – to define
units for distance, time interval and mass. We have innummerable possibilities for
choice of definitions of these units, but the interesting question is: Does there exist
a universal and absolute system of units, independent of living creatures and specific
local systems? My reply to this question is: Yes! A yes, because I believe to have
found these absolute cosmological fundamental units!We shall revert to these cosmological units, but first we shall look at some
remarks to the measuring units we normally use in our physical description of the world.
Almost all countries have agreed to use the same physical units, which are: the distance
meter, the time second and the mass unit kilogram. Previously there was chaos regarding
basic units, different units were used in different countries, sometimes even different
units were used within the same country.
The basic units used today, meter, kilogram and second, are far from being cosmologic,
on the contrary they have an origin tightly connected to the human dimensions and rhytms.
One meter is approximately equal to the length of a leg of an adult person. One second
is approximately equal to the interval between two pulse beats, and a kilogram is
approximately equal to one third of the weight of a newly born baby. Gradually it was realized that it was practical to define the physical basic units
independent of human relations. As an example, the unit of length, one meter, was
introduced during the French revolution, and in 1791 it was defined as one ten millionth
of the distance between the North Pole and Equator, measured along the longitude circle
through Paris. Based on measurements of degrees, a standard was manufactured of platin,
the so-called archive meter. This should then be a secondary normal meter.
Later measurements have shown that the archive meter is 2/10 mm shorter than
1/107 of the length of the earth quadrant. The archive meter was then
chosen as primary normal meter, and the meter was defined as the distance between the
two plane ends of the platine stick at 0° Celcius. Thus there is no more connection
between the meter and the nature object Earth. Since then the meter was adjusted and
defined several times. At the 11th General Conference for Measure and Weight in Paris
1960 a new definition was given. This definition is determined by a definite emission
of photons from the krypton-86 atom. It was decided: One meter is 1650763.73 times the
wavelength in vacuum of the emission by a jump from level 2 p10 to
5 d5 in the atom.
Stoney's and Planck's "Units"
At a meeting in Belfast in 1874, the Irish physicist George Johnstone Stoney
(1826-1911) ['On the Physical Units of Nature', Philosophical Magazine, vol. 11, p. 381
(1881)] forwarded a proposal to some "natural" units for length, time and mass,
independent of human existence. By suitable combinations of Newton's gravitation constant,
the velocity of light and an electric unit for charge, which Stoney had himself proposed
and calculated, he could construct a length, a time and a mass.Stoney found the following values:
Length = 10-37 meter, time = 0.3 × 10-45 second
and mass = 10-7 gram.
It should be noted that the electron was only discovered in 1897 and that 'electron'
was introduced by Stoney as the name of the smallest electrolytic unit of charge.
Likewise is should be noted that Stoney's units are introduced purely ad hoc
without connection to any theory. In 1899 Max Planck (1858-1947) ['Über irreversible Strahlungsvorgänge'.
Sitzungsberichte der Preußischen Akademie der Wissenschaften, vol. 5, p. 479 (1899)]
gives a mathematical description of the electromagnetic radiation from an 'absolutely
black body'. In order to be able to explain the experimental facts, Planck had to break
with the classical continuous physics, and had to presume that the radiation was emitted
in discrete energy portions – called quanta. After the introduction of his quantum constant, Max Planck showed, by a pure
consideration of dimensions, that it was possible to construct a length, a time and
a mass, by means of Newton's gravitation constant, the velocity of light and the new
Planck constant. The energy of one radiation quantum was proportional to the frequency of a specific
radiation. This proportionality constant, connecting the energy of a quantum and the
frequency, we today call Planck's Constant. By the quantization of the radiation energy
and the introduction of Planck's Constant, quantum physical considerations were introduced
in the description of nature. The equations for calculation of what we today call Planck length lp,
Planck time tp and Planck mass mp are given by:
(p1) 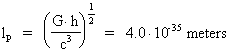
(p2) 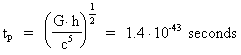
(p3) 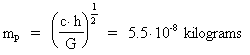
In these equations, G is Newton's gravitation constant, h Planck's constant, and c is
the velocity of light.
Using Boltzmann's thermo-dynamic constant k, Planck also constructed an extremely
high temperature:
(p4) 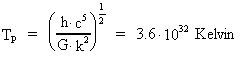
The quantities defined by the expressions (p1) to (p4) are constructed ad hoc, without
connection to any theory, and Max Planck himself was very much against discontinuous
physics. Today several cosmologists use these Planck quantities for conditions in the early
Universe, and this in spite of the fact that the quantities can not be motivated as being
fundamental for any physical theory. The motivation for their use is their small size,
but nobody has foreseen the small elementary quantities from my theories.
Elementary Length and Elementary Time
Quantization of Space and Time
The space quantum – elementary length r0 – is given by:
(1) 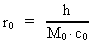
where h is Planck's constant, M0 the total matter/energy mass of the
Universe and c0 the velocity of light in a field free vacuum. I shall call
this the light constant.
The time quantum – elementary time t0 – is given by:
(2) 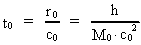
The mass of an "elementary particle" is presumed to be a definite fraction
of the total mass of the Universe. As an example we have for the gravitational mass
me of an electron:
(3) 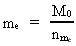
where I shall call nme the electron's mass quantum number.
This is an extremely great number.
In a rational quantum physics, the following is valid:
Each physical finite distance 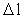 is equal to
a natural number, the space quantum number is equal to
a natural number, the space quantum number 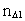 multiplied
by elementary length r0, we have: multiplied
by elementary length r0, we have:
(4) 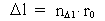
Likewise: each physical time interval 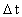 is
equal to a natural number – the time quantum number is
equal to a natural number – the time quantum number
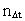 multiplied by elementary time t0. Thus multiplied by elementary time t0. Thus
(5) 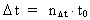
All physical quantities, such as velocity, acceleration, force, work, energy etc. are
defined as usual, but we must take in account the quantization of space, time and mass.
This fundamental "atomization" causes that all movement is discontinuous –
all movements are "jumps". Likewise all physical processes in a definite system
will be characterized by discontinuous changes of certain physical quantities. Processes in a physical system we can describe by changes of certain quantum numbers,
belonging to certain physical quantities, and for these quantum numbers certain
conservation laws are valid. All physical quantities can be expressed by the cosmical fundamental quantities:
the space quantum, the time quantum and the total matter/energy mass of the Universe!
The Quantum Cosmological Basic Equations
The Evolution Quantum Number
Click here for a summary of my holistic quantum cosmology. The above theory gives a connection between the actual extension of the Universe, its
actual age and elementary length and elementary time. Likewise it gives a connection
between the total matter/energy mass and the elementary mass at any time. The coupling
quantity connecting the extension of the Universe, its age and mass, I call the cosmic
evolution quantum number. This cosmic evolution quantum number 'ticks' up through the
range of natural numbers. The Universe was 'born' when the cosmic evolution quantum
number had the value 1! The cosmic evolution quantum number determines the strength of the relation between
the electrostatic and the gravitostatic forces, existing at any time between an electron
and a positron. In the embryonic phase of the Universe, these forces were equal.
The quantum cosmological basic equation can now be written as follows:
(6) 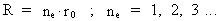
(7) 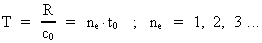
(8) 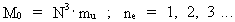
In the equations, R is the actual extension of the Universe, T is the corresponding age,
M0 is the total matter/energy mass of the Universe and m0 the
elementary mass, valid for R (or T). It should be noted that the two last equations can
be deducted from equation (6).
ne is the cosmic evolution quantum number, which also "controls"
the relations between the electrostatic and gravitostatic forces, viz.:
(9) 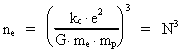
where kc is the Coulomb constant, e the electric elementary quantum,
me the gravitational mass of the electron, mp the gravitational mass
of the positron and G the actual value of the gravitational "constant", which
varies as the cosmic quantum number "ticks" up through the natural numbers.
From equation (9) it will be seen that G decreases while the Universe is quantized
up in size. The following is valid:
(10) 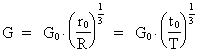
as the original gravitational "constant" G0 is given by:
(11) 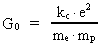
The connection between G0 and G can thus be written as:
(12) 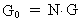
Spaton, tempon, and masson,
the absolute units of the Universe.
The existence of the physical elementary quantities, elementary length,
elementary
time and elementary mass, denoted by r0, t0 and m0
respectively, shows the existing possibility for introduction of some absolute and
fundamental units for the physical basic quantities, distance, time and mass.
Let us decide the following:
- Elementary length defines a distance unit: 1 spaton, for short 1 [sp]
from latin spatium, space
- Elementary time defines a time unit: 1 tempon, for short 1 [te]
from latin tempus -oris, time
- Elementary mass defines a mass unit: 1 masson, for short 1 [ma]
from latin massa, lump
The cosmological units 1 spaton and 1 tempon are absolute and invariant, viz. they are
independent of the evolution of the Universe, and likewise they are independent of
living creatures and specific local systems. As they are thus independent of our
existence, they can also not be dependent on how we as observers move in relation
to each other. As the ratio between r0 and t0 so to speak define
the velocity of light c0, it is seen that this is the same for all observers.
The cosmological mass unit, 1 masson, is on the other hand a variable unit, as it must be
assumed that the product of elementary mass and the cosmic evolution quantum number is
constant, equal to the total matter/energy mass of the Universe. Elementary mass
decreases as the Universe develops.
Physical quantities and their evolution equations in cosmological units
In the following we shall look at some physical quantities and their values, given in
cosmological units. As the light constant c0 is given by the ratio between
elementary length r0 and elementary time t0, we have:
(13) 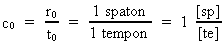
In cosmological units we have for the extension of the Universe R, its age T and its
mass M0:
(14) 
(15) 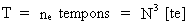
(16) 
We note interestingly that the characteristic universal quantities R, T and M0
are taking the same number, namely the cosmic evolution quantum number, when expressed
in the cosmological units. When the Universe was 'born', they all had the value
1 (one)!!
The Planck value and its evolution equation in cosmological units
In cosmological units, Planck's "constant" is variable. From equation (1) we
get:
(17) 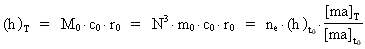
where we have also used equations (8) and (9). [ma]T gives the cosmological
mass unit at the time T, and [ma]t0 at the time t0
when the Universe was "born". Equation (17) is thus an evolution equation for
the Planck quantity. On the other hand, (h)t0 = 1, viz. the Planck
"constant" had the value 1 when the Universe was "born"!
(h)t0 is thus an increasing discrete function, increasing
in accordance with the quantum expansion of the Universe.
The gravitational mass of an electron and its evolution equation
Let us assume that the gravitational mass of the electron can be calculated as a
fraction of the total matter/energy mass of the Universe, M0. Thus we have:
(18) 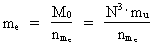
where the cosmic mass quantum number of the electron, nme is
assumed to be constant in all unit systems. To the two "times" T and
1·t0 we thus get for the mass conditions of the electron:
(19) 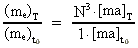
In equation (19), [ma]T gives the cosmological mass unit to time T and
[ma]t0 gives it to time t0. As mentioned before,
these mass units are different. The following evolution relation is valid for
the mass of the electron:
(20) 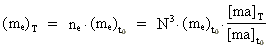
The electric elementary quantum and its evolution equation
We shall now study how the evolution of the electric elementary quantum goes.
For this purpose we shall first redefine the electric elementary quantum e so
that it can be expressed exclusively by the "mechanical" basic units for
distance, time and mass. We introduce the Coulomb constant kc and define
an electric elementary quantum qe by:
(21) 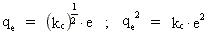
The SI unit for this electric charge is (m/s)·(kg·m)1/2, thus a
unit with a fractional exponent. To the two "times" T and t0 the
following is valid:
(22) 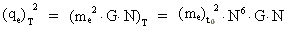
(23) 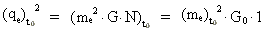
where G0 is the value of G at the time 1·t0 and where the
figure 1 marks that N is equal to 1 at the same time.
For the electrical elementary quantum (qe)T we get the following
evolution equation:
(24) 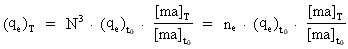
We see again that the cosmic evolution quantum number determines the evolution.
The fine structure "constant" and its cosmological evolution equation
With the previous results it can easily be shown that the so called fine structure
"constant" 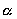 has the following evolution
equation in cosmological units: has the following evolution
equation in cosmological units:
(25) 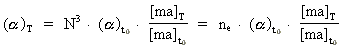
viz. the same mathematical formula expression as valid for the other physical quantities,
which are characteristic for the phenomena in our Universe.
Theoretical deduction of the universal decrease of gravityA fundamental theoretical question within physics is: Is there a variation in space
and time of the physical quantities, which we a priori assume being nature constants?
Is there f.i. a variation of Planck's constant, the mass of the electron, the electric
elementary quantum, the velocity of light or Newton's gravitation constant, as the
Universe is gradually developing? Or are these quantities constant in space and time? In the previous parts of this paper I have shown that in the cosmological units,
where the cosmological mass units vary with the disintegration of the Universe in
smaller and smaller mass quantities, in this system of units some of the physical
coupling quantities vary. The variation of Newton's gravitation "constant"
will appear after the following considerations, where it will be shown that the
variation of this is different from the variation of other physical quantities.
Let us define a gravitational mass mg, using Newton's gravitation 'constant'
G and the mass me of the electron, so that:
(26) 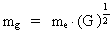
It can be shown that for mg the following evolution equation is valid,
given in cosmological units:
(27) 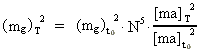
We see that the development factor in equation (27) is N5, and thus it is
different from the development factors for the other physical quantities I have
described.
In cosmological units, this defined gravitational mass is increasing, but let us now
transform to other, but fixed physical units. This we can do by means of the
following connection between N and the cosmological mass units to the "times"
T and 1·t0
(28) 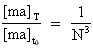
Using equation (28) in (27) we get:
(29) 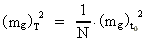
This equation is valid in an arbitrary unit system with fixed invariant basic units.
From equation (29) we see the interesting, that the redefined gravitational mass² of
the electron, mg² decreases reverse proportional to N. By means of
equation (6) and (9) we can express the variation by the actual extension of the
Universe R. We get:
(30) 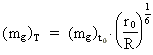
This equation we could also have found from equation (10). On the other hand, we can now
from equation (30) and equation (26) get equation (10), viz.
(31) 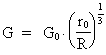
In equation (31), G is the gravitational "constant" at the "time" T
and G0 the value at "time" 1·t0, viz. when the
Universe was "born".
If we transform the equations (17), (20), (24) and (25) to a system of units with fixed
basic units, as f.i. the usual SI unit system, by means of the expression in equation
(28), we get the following:
(32) 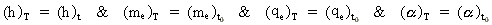
showing that these quantities do not vary as the Universe develops. On the other
hand it has been shown that Newton's gravitational "constant" decreases, as
the Universe expands in quantum "jumps".
If we denote the ratio 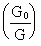 with the Greek letter
gamma, viz. with the Greek letter
gamma, viz.
(33) 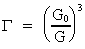
we can get the same evolution equation as for the other physical quantities, namely:
(34) 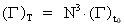
It should, however, be greatly underlined, that the evolution equation in (34) is valid
in all unit systems, as it does not depend on the ratio between the
cosmologic mass units, as the case is for the evolution equations, I have deducted for
the other quantities.
The quantum holistic formula for the Universe and its evolution through natural numbers
The previous analyses can now be collected to a universal whole, as I have shown
that in the cosmological units there is the following context between the physical
quantities defined by us men to be able to describe the Universe from which we have
developed:
(35) 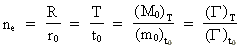
(36) 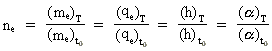
In these equations ne is the cosmic evolution quantum number which can
only take natural numbers. The Universe develops in "quantum jumps",
as ne "ticks" up through the natural numbers. The Universe was
"born" when ne took the value 1. Equations (35) and (36) are the
evolution equations of the Universe.
The only universally constant physical quantities are: elementary length,
elementary time and the light constant. These have only the value 1 in cosmological units.
We can formulate equations (35) and (36) in a universal equation: the
quantum holistic formula of the Universe.
(37) 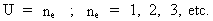
where U can be 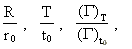 etc. etc.
Hereby microcosmos has been combined with macrocosmos, the smallest with
the greatest.
Maximum values of the age and extension of the Universe
and its jump towards obliteration
An interesting question is: Does the Universe have a maximum
lifetime, and in the affirmative, what is the maximum age? Within my
holistic quantum cosmology a possibility exists to give an answer to this.
According to this theory, matter and energy of the Universe is split in
smaller and smaller matter/energy quanta, corresponding to a smaller and
smaller elementary mass. Together with this break-down of
matter and energy, the gravity decreases and the Universe increases in
geometrical size, in order that matter and energy can be distributed according
to the entropy law.
The possibility to calculate the maximum lifetime of the Universe is hidden
in the constant decrease of gravity. Calculating in the cosmological
units, which I have introduced, we find that the gravitational 'constant'
started with an extremely high value when the Universe was 'born', and has
today decreased to a much smaller value, however greater than 1.
When the Universe was 'born', the gravitational 'constant' G0 had
the value:
(38) 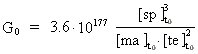
The gravitational 'constant' today — in our epoch — is calculated
to be:
(39) 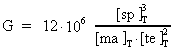
which shows that the gravitational 'constant' started with an extremely
high value when the Universe was 'born', while it today has decreased
considerably. It must be assumed that the gravitational 'constant' will
continue to decrease, until it reaches the value 1, but not farther to 0
or negative figures, as this will mean that we get non-acceptable
physical conditions.
From (38) and (39) we get:
(40) 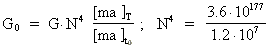
If we set G = 1 in equation (40) we get the maximum value of N, viz.:
(41) 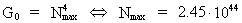
Inserting this maximum value in the cosmological basic equation for the age
of the Universe, viz. the equation:
(42) 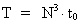
we get:
(43) 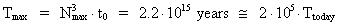
Using equation (7), the maximum extension of the Universe can be calculated:
(44) 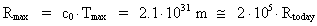
From the quantum cosmological equation (8) we can calculate the smallest
value of the quantum mass, with which the Universe will 'close' and
'extinguish'.
If the Universe then will 'jump' to obliteration, or the cosmic quantum
number will start 'ticking' backwards, the future must show!
January 1997Louis Nielsen
louis44nielsen@gmail.com
Next article
Main entry
|