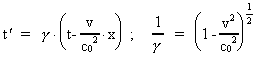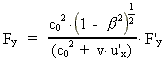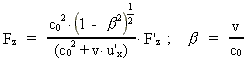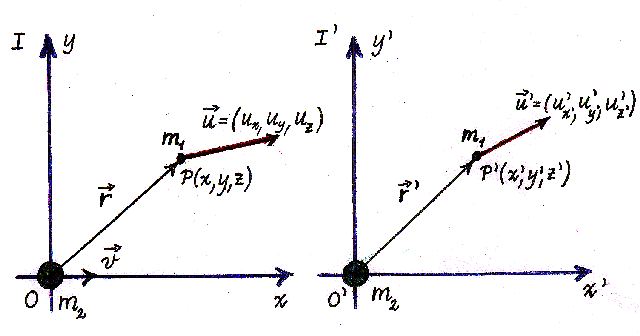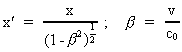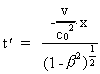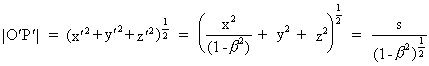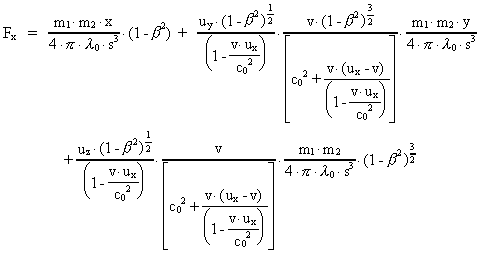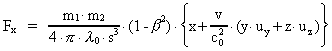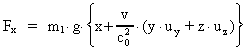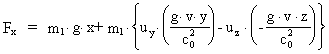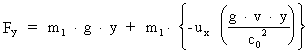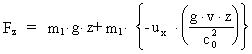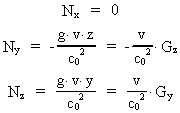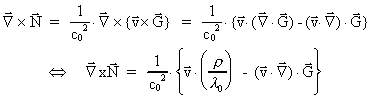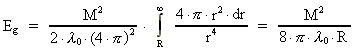|
A Maxwell Analog Gravitation Theory
With Two Gravitational Fields
by Louis Nielsen
Senior Physics Master, M.Sc.
E-mail: louis44nielsen@gmail.com
Introduction
I shall in this article show that the gravitational rotation field, which
I introduced in an earlier article (Louis Nielsen,
 Gamma No. 9, 1972, Niels Bohr Institute, Copenhagen), is a consequence
of the special theory of relativity.
Gamma No. 9, 1972, Niels Bohr Institute, Copenhagen), is a consequence
of the special theory of relativity.
The calculations are used to show that the magnetic induction field is a
relativistic correction to electrostatics. It can namely be shown that
Maxwell's equations are a consequence of:
- Coulomb's electrostatic forces,
- the special theory of relativity, and
- the invariance of electric charge.
Likewise it has been shown that the origin of the magnetic induction field
is found in the relativistic Thomas rotation. An analog argumentation leads
to the existence of a gravitational rotation field.
Deduction of the gravitational equations
I shall now deduct the field equations, which must be fulfilled by
the gravitostatic field
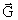 and the gravitational rotation field
and the gravitational rotation field
 .
I shall use the following starting points and assumptions: .
I shall use the following starting points and assumptions:
a) Newton's gravitostatic force law,
b) the transformation equations for positions, times, velocities,
and forces of the special theory of relativity, and
c) the assumption that the gravitational mass is Lorentz invariant.
Ad a):
Newton's force law for resting gravitational charges (equal to
gravitational masses) I shall write as follows:
(1) 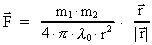
where m1 and m2 are the gravitational forces
between two particles, r the distance between them, and
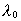 a negative
parameter, connected to Newton's gravitational constant G by the formula: a negative
parameter, connected to Newton's gravitational constant G by the formula:
(2) 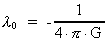
We shall everywhere use the SI unit system. As we do not have a
minus sign in (1), 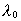 must necessarily be negative for the gravitational masses, as we know them
in our part of the Universe. Our experience tells us that gravitational
masses with the same sign attract each other.
must necessarily be negative for the gravitational masses, as we know them
in our part of the Universe. Our experience tells us that gravitational
masses with the same sign attract each other.
We see that equation (1) is mathematically identical to Coulomb's
force law for resting electrical charges:
(3) 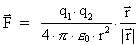
where now q1 and q2 are the electrical charges, and
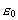 the
dielectricity constant in vacuum. The physics behind equations
(1) and (3) is not identical. This f.i. corresponds to the fact
that the physics behind water waves and electromagnetic waves is not
identical, but the mathematical description is identical.
Another example among many, where the mathematical structure is identical,
but the physics different, can be found in the phenomena spin and isospin.
This mathematical isomorphism (same form) is an experience which should
be remembered. the
dielectricity constant in vacuum. The physics behind equations
(1) and (3) is not identical. This f.i. corresponds to the fact
that the physics behind water waves and electromagnetic waves is not
identical, but the mathematical description is identical.
Another example among many, where the mathematical structure is identical,
but the physics different, can be found in the phenomena spin and isospin.
This mathematical isomorphism (same form) is an experience which should
be remembered.
Ad b):
We shall assume that we can use the transformation equations of the special
theory of relativity. We shall use the Lorentz transformation:
(4) 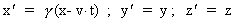
(5) 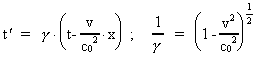
and the transformation equations for the components of force:
(6) 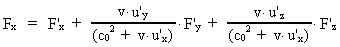
(7) 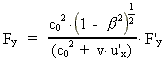
(8) 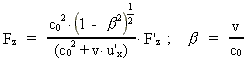
The unmarked quantities are measured in the inertial frame I, the
marked in the inertial frame I', which moves with the velocity v
along the X-axis of I. u' is the velocity of a particle
in I'. The quantity c0 is a nature constant, corresponding
to the velocity of a photon in field free vacuum. By field free
vacuum I shall understand a domain of space, absolutely free from both
fields and matter.
Besides equations (4) to (8) we shall use the transformation equations
for velocities.
Ad c):
The assumption that the gravitational mass is Lorentz invariant collides
with the equivalence principle. – The equivalence principle can be
formulated as the principle that the inertial and the gravitational
masses are identical.
As the inertial mass increases by velocity, the gravitational mass will
also increase in the same way. This seems intuitively to be very strange.
Let us consider two initial systems, I and I'.
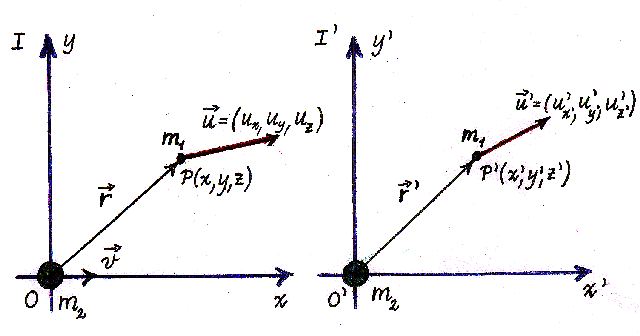 In the inertial frame I the gravitational mass m2
is moving with velocity v. The inertial frame I' is moving with
velocity v in relation to frame I and along this frame's X-axis.
The mass m2 will then be at rest in frame I', and we
shall presume that it is situated at the origo O', the starting point for
I'. We shall calculate the force on a particle with the mass
m1, with at the time t=0 is situated in the point P, measured
in relation to the frame I. The particle m2 is then just
in the point O in the frame I. At the time t=0 the mass m1
has the velocity
In the inertial frame I the gravitational mass m2
is moving with velocity v. The inertial frame I' is moving with
velocity v in relation to frame I and along this frame's X-axis.
The mass m2 will then be at rest in frame I', and we
shall presume that it is situated at the origo O', the starting point for
I'. We shall calculate the force on a particle with the mass
m1, with at the time t=0 is situated in the point P, measured
in relation to the frame I. The particle m2 is then just
in the point O in the frame I. At the time t=0 the mass m1
has the velocity
 = (ux,
uy, uz) in frame I and similarly = (ux,
uy, uz) in frame I and similarly
 ' = (u'x,
u'y, u'z) in frame I'.
In the inertial frame I' we have at time t=0 in frame I: ' = (u'x,
u'y, u'z) in frame I'.
In the inertial frame I' we have at time t=0 in frame I:
(9) 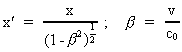
(10) 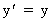
(11) 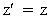
(12) 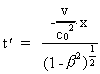
From here we get the distance |O'P'|:
(13) 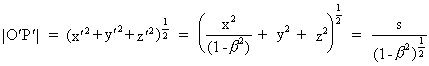
where s is defined by: s = (x² + (1-ß²) ·
(y² + z²))1/2
The numerical value of the force F' on the mass m1 in
point P' will at the time t' = - v/c0²·x·(1-ß²)-1/2,
corresponding to time t=0 in system I be given by:
(14) 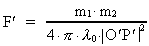
or in components along the x'-, y'-, z'-axes:
(15) 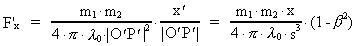
(16) 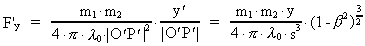
(17) 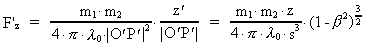
Inserting (15) in the transformation equation (6) we get:
(18) 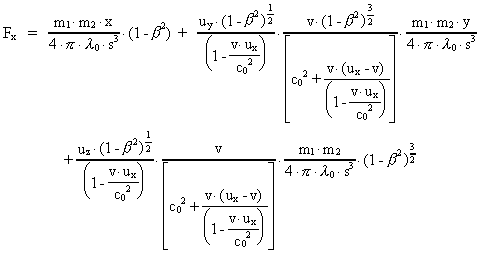
This can be written as:
(19) 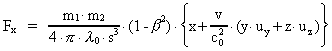
or:
(20) 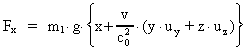
where g is defined by:
(21) 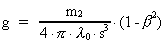
For the other components we get by means of the transformation equations:
(22) 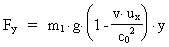
(23) 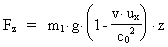
Equations (20), (22) and (23) give the force components as measured in
the inertial frame I. We see that the force between the particles
depends on their velocities in frame I.
Equations (20), (22) and (23) now allow us to define a new gravitational
field in such a way that it can be expressed by a gravitational force law,
as follows:
(24) 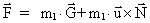
or written in components:
(25) 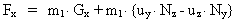
(26) 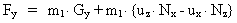
(27) 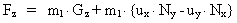
Writing equation (20) as:
(28) 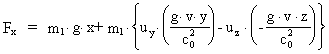
and comparing with (25), we conclude that the
 -field is defined by: -field is defined by:
(29) 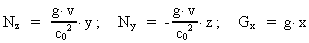
Likewise we get by comparing the equation:
(30) 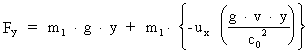
by (26):
(31) 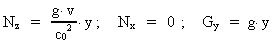
Finally we compare:
(32) 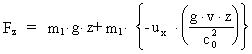
with (27), and get:
(33) 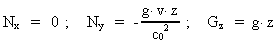
We have thus shown that in the inertial field I the
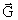 -field is determined by: -field is determined by:
(34) 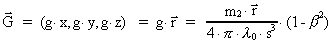
where 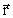 is the position
vector for the point P.
We see that the is the position
vector for the point P.
We see that the 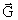 field depends on the velocity v, whereby the mass m2 is moving
in relation to system I.
field depends on the velocity v, whereby the mass m2 is moving
in relation to system I.
Collecting the components for the
 -field we get: -field we get:
(35) 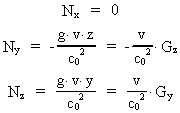
and, we see that it has the nature of a rotation field. The equations in
(35) mean that the following vector equation is valid:
(36) 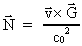
We can now set up a rotation equation for the
 -field,
operating with the rotation vector -field,
operating with the rotation vector
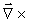 on both sides of the equation sign in (36).
on both sides of the equation sign in (36).
We get:
(37) 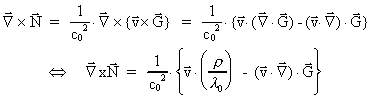
The last term in (37) we can rewrite as follows:
As 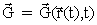 follows
from this, that the total derivative of follows
from this, that the total derivative of
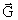 is given by: is given by:
(38) 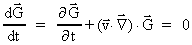
which gives the change of
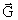 per time unit,
if we follow the field, which is then constant. per time unit,
if we follow the field, which is then constant.
The total derivative is thus zero, and we get:
(39) 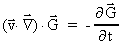
which inserted in (37) gives:
(40) 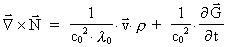
By introduction of "the gravitational permeability of vacuum"
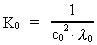 and the
vector for mass current density and the
vector for mass current density
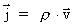 we finally get the equation:
we finally get the equation:
(41) 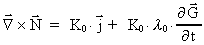
In equation (37) we have used that:
(42) 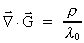
which is an equivalent, but still more general equation than Newton's
gravitostatic force law (1). Equation (42) can be understood as follows:
Let the mass m2 be placed in the center of a sphere with
radius r. On the surface the
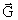 -field
is radial and given by: -field
is radial and given by:
(43) 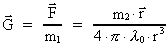
Integrating over the sphere and using Gauß's integral theorem we get:
(44) 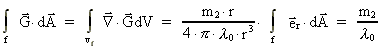
At the limit to a small volume around m2 we get (42) as:
(45) 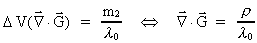
We now only need equations for 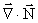 and and 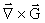 . .
As an assumption, but definitely not sure, we shall consider the
 -field as free of
sources, viz. as a pure whirl field. We thus assume that the divergence
of the -field as free of
sources, viz. as a pure whirl field. We thus assume that the divergence
of the
 -field is
negligible, which means: -field is
negligible, which means:
(46) 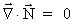
It is quite possible that
 -field monopoles
exist, and (46) must then be modified as: -field monopoles
exist, and (46) must then be modified as:
(47) 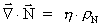
where 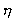 is a constant,
and is a constant,
and 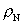 is the density
of the is the density
of the  -field monopoles. -field monopoles.
We shall now deduct an equation for
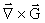 .
We could now go back to the original transformation equations and deduct .
We could now go back to the original transformation equations and deduct
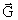 expressed by expressed by
 and and
 .
We shall not do that, but simply give the result: .
We shall not do that, but simply give the result:
(48) 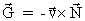
An argument for equation (48) might be formulated by the force law,
equation (24).
Let there be given an
 -field,
and let us consider a definite point within it. Let a particle arrive
to this point and here have the velocity -field,
and let us consider a definite point within it. Let a particle arrive
to this point and here have the velocity
 .
This requires that the .
This requires that the
 -field in
the point shall change in time in a way so that the force on the particle
is zero. If we assume that a change of the -field in
the point shall change in time in a way so that the force on the particle
is zero. If we assume that a change of the
 -field in time is
introducing a -field in time is
introducing a
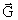 -field, we see from (24)
that -field, we see from (24)
that
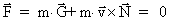 , which gives
(48). By operation with the rotation operator , which gives
(48). By operation with the rotation operator
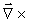 we get from (48): we get from (48):
(49) 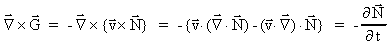
as 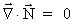 and and
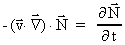 . .
I have hereby shown that the special theory of relativity requires
the existence of two gravitational vector fields characterized
by the 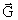 -field and the -field and the
 -field. -field.
I have thus demonstrated that the following equations must be valid
(pending the absence of  -field
monopoles): -field
monopoles):
(50) 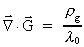
(51) 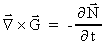
(52) 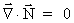
(53) 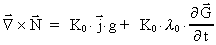
together with the force law defining the
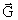 - and - and
 -fields: -fields:
(54) 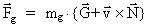
These equations are in their primary structure mathematically identical to
Maxwell's electrodynamic field equations for the electric
 -field
and the magnetic induction field -field
and the magnetic induction field
 ,
as these fields obey the equations: ,
as these fields obey the equations:
(55) 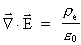
(56) 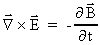
(57) 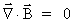
(58) 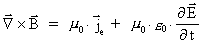
together with the force law, defining the
 - and - and
 -fields: -fields:
(59) 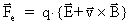
Here
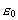 is the
dielectric constant of vacuum and is the
dielectric constant of vacuum and
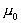 the magnetic permeability
of vacuum, the magnetic permeability
of vacuum, 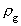 is the
gravitational mass density, and is the
gravitational mass density, and
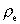 the
electrical charge density. the
electrical charge density.
Cross references:
- A two-vector field gravitation
theory with variable coupling »constants«
- Centrifugal and Coriolis forces are
identical to the N¯ field
Non-linear field equations. Introduction of
negative gravitational masses
In spite of the primary mathematical resemblance between the two
theories, expressed by the two sets of equations (50) to (54) and (55)
to (59), the physical difference, however, is great. Maxwell's
electrodynamical theory is linear while the present theory is
non-linear. This non-linearity is a consequence of Einstein's
mass-energy relation, coupled with the equivalence principle. Einstein's
mass-energy relation tells that any energy E has an inertia corresponding
to an inertial mass mi given by:
(60) 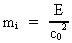
This is a result of the special theory of relativity and is thus only
relating to the inertial mass. The equivalence principle, which is
basical for Einstein's general theory of relativity, can be formulated
as follows:
If a particle has an inertial mass mi then there will to this
particle also be attached an equivalent gravitational mass mg
of the same size as mi, viz. the following is valid:
(61) 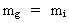
This result means that to every energy E there is also attached an
equivalent gravitational mass mg given by:
(62) 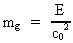
As there is, in the gravitational field, an energy density this
corresponds to an equivalent mass density as given by (62). This
mass density causes a new gravitational field etc.
This special interchange between field and mass causes that the
gravitational field equations become non-linear. We shall investigate
this below. We shall, for simplicity, consider a resting
gravitational mass mg. This mass is creating a gravitostatic field
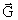 according to
the equation: according to
the equation:
(63) 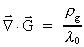
It can be shown that this field (similar to the field around a resting
electrical charge) contains an energy density Ug given by:
(64) 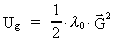
As 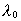 is negative,
we see that the energy density in the field is negative. According
to (62) this corresponds to a negative gravitational mass density: is negative,
we see that the energy density in the field is negative. According
to (62) this corresponds to a negative gravitational mass density:
(65) 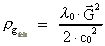
If (62) is exact and valid we must conclude that negative gravitational
masses exist. This result is highly interesting and simultaneously it
fulfils our sense for symmetry. If the interpretation is true can,
however, be discussed. The equivalence principle, as expressed by
equation (61) causes that a negative gravitational mass must also have
a negative inertial mass, which seems to be rather remarkable.
If (61) is generally valid, negative inertial masses must be the
consequence of negative gravitational masses.
The mass density (65) gives raise to a
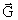 -field which couples
with the original, so that the total -field which couples
with the original, so that the total
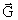 -field must be
determined by the equation: -field must be
determined by the equation:
(66) 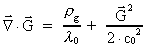
Equation (66) is a non-linear differential equation, which causes that it is
rather complicated to solve. If the gravitational fields are relatively weak,
the equations can be linearized. F.i. the last term in (66)
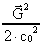 will be vanishing in comparison with
will be vanishing in comparison with
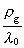 ,
if we consider the Earth. ,
if we consider the Earth.
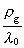 will be of the order
10-5 and
will be of the order
10-5 and 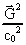 of the order 10-14.
of the order 10-14.
It could now be interesting to calculate how much negative mass the
gravitostatic
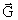 -field around the
Earth is equivalent to. The energy density Ug
(J/m³) is, in the distance r from the center of the Earth, given by: -field around the
Earth is equivalent to. The energy density Ug
(J/m³) is, in the distance r from the center of the Earth, given by:
(67) 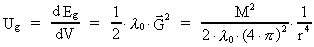
as
(68) 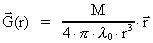
By integration from the surface of the Earth to infinity we get for the
total energy Eg in the field:
(69) 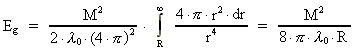
Here R is particle radius (radius of the Earth) and M particle mass
(mass of the Earth). As we note
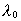 is
still negative, and the total energy in the field is negative.
Expressed by Newton's gravitational constant G we can write: is
still negative, and the total energy in the field is negative.
Expressed by Newton's gravitational constant G we can write:
(70) 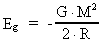
This expression formally corresponds to the potential energy of a particle
with the mass M, being in the distance 2·R from another particle,
also with the mass M. The energy (70) is equivalent to a negative
gravitational mass:
(71) 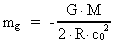
Using the values M = 1024 kg, R = 6·106 m,
G = 6.6·10-11 Nm²/kg² we get a negative mass
of the order mg = -1014 kg.
Interaction between positive and negative masses
In this section we shall investigate how negative and positive masses
interact. Premarily we shall assume that the equivalence principle is valid.
This causes, as earlier mentioned, that a negative gravitational mass must
be allocated a negative inertial mass. Let us consider a positive
gravitational mass mg being in a field from a fixed positive
gravitational mass Mg.
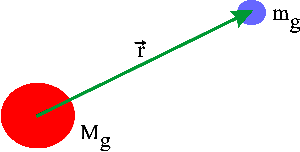
The equation of motion for mg is given by:
(72) 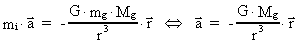
which gives an acceleration 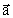 towards Mg. towards Mg.
Now we consider a negative gravitational mass -mg which
will have the equation of motion:
(73) 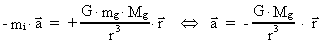
which also gives an acceleration towards Mg.
Now let us consider a negative gravitational mass -Mg which is
fixed (f.i. by means of supporting forces). Let in the field first a
positive, then a negative mass move.
The positive mass has the equation of motion:
(74) 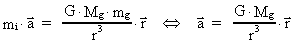
and thus an acceleration
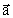 way from the
mass M. The negative mass has the equation of motion: way from the
mass M. The negative mass has the equation of motion:
(75) 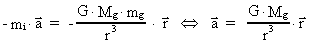
which also means an acceleration away from Mg.
The results of (72) to (75) are based on the assumption that the
equivalence principle is valid so that se must operate with negative
inertial mass. If we limit the equivalence principle to be valid only
for positive gravitational masses and thus furnish a negative
gravitational mass with a positive inertial mass, then we get the
following interaction: gravitational masses with the same sign attract
each other, whereas masses with different sign repulse.
In the previous section we considered a resting gravitational mass. If
a gravitational mass moves in relation to an observer, there will besides
the 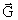 -field
also be an -field
also be an
 -field.
The energy density Ug, which is in the field, is then given by: -field.
The energy density Ug, which is in the field, is then given by:
(76) 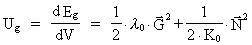
As K0 is also negative, the energy density given by (76)
will also be equivalent to a negative mass.
Next article
Main entry
|