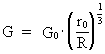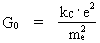I det følgende vil jeg vise, at de virkninger vi kalder 'inerti' og 'gravitation' er intimt forbundne, og at dette er en konsekvens af min 'Holistiske kvantekosmologi' (se denne). En følge af denne er, at der 'overalt' i universet eksisterer nogle fysisk mindste elementære diskrete energi-/stof kvanter som jeg kalder unitoner. Eksistensen af et allestedsnærværende 'kosmisk unitonhav' bestående af unitoner, der bevæger sig i alle mulige retninger med uhyre store hastigheder, kan give en mekanisk forklaring af både gravitations-kræfter og inerti-kræfter. Jeg viser andetsteds, at uniton-temperaturen af det kosmiske unitonhav i vor epoke er yderst tæt på det absolutte temperaturnulpunkt. Det vi kalder 'stof' er 'unitonfortætninger' i det uhyre kolde kosmiske unitonhav og kan betragtes som Bose-Einstein kondensater! Eksempelvis er en elektron et uniton-dynamisk subsystem, der er i vekselvirkning med det kosmiske uniton-felt. Elektriske kræfter kan derfor også føres tilbage til at være vekselvirkninger mellem unitoner. Se ' Ny kosmologisk model af elektronen'.

Hvis massestørrelsen af en given 'stofportion' defineres som værende ligefrem proportional med antallet af unitoner, hvoraf 'stofportionen' består, da kan dette give en uniton-mekanisk forklaring af, hvorfor den såkaldte inertielle masse er lig med den såkaldte gravitationelle masse og dermed hvorfor inerti-kræfter og gravitations-kræfter er ækvivalente. Min påstand: Både inerti-kræfter og gravitations-kræfter forårsages af mekaniske vekselvirkninger mellem de unitoner som et givet legeme består af og unitonerne i det kosmiske unitonhav. En sådan sammenhæng er i overensstemmelse med det såkaldte 'Machs princip'.

Den geometriske udstrækning af én uniton svarer til den fysisk mindste 'afstandsmåle-enhed' .Denne har jeg givet navnet 'en spaton'. En uniton er i 'besiddelse' af den aktuelt mindste energimængde og dermed mindste kraftvirkning. Jeg giver en definition af 'tid', der er baseret på forandringer i et natureksisterende system. Med et stadigt voksende antal af unitoner i universet kan dette give os en meningsfyldt og entydig definition af den størrelse vi kan vælge at betegne med ordet 'kosmisk tid', At den kvantiserede kosmiske tid, der svarer til universets aktuelle alder, 'forløber' i en bestemt retning -kaldet 'tidens pil' - kan forklares derved, at antallet af unitoner i universet til stadighed forøges. I det følgende defineres den 'kvantiserede kosmiske tid' som værende ligefrem proportional med det aktuelle antal unitoner i universet.

Hvis den totale kosmiske entropi defineres, at være ligefrem proportional med uniton-antallet i universet, kan dette forklare, hvorfor entropien i universet er stadigt voksende!

Grundlaget for min holistiske kvantekosmologi og holistiske kvantefysik er følgende kosmo-holistiske formel der forener de mikrofysiske og makrofysiske konstanter:

(1)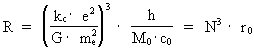

I ligning (1) er R universets aktuelle udstrækning, k_C er Coulomb konstanten, e elektronens elektriske ladning, m_e elektronens gravitationelle masse og G den aktuelle talværdi af Newtons gravitations'konstant', der i min teori er en diskret aftagende størrelse. N angiver således størrelsen af det aktuelle forhold mellem de elektrostatiske - og gravitostatiske kræfter mellem to elektroner. N³ spiller rollen som et diskret kosmisk evolutions kvantetal der 'tikker' op igennem de naturlige tal. Da universet blev født antog N³ tallet et.

r₀ er universets fysisk mindste afstand - elementarlængden - og er sammenknyttet med Plancks konstant h, lysets fart c₀ i såkaldt vacuum og universets totale energi-/stof masse M₀ ved følgende formel:

(2)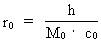

Ligning (1) skal udtrykke, at universets fysiske udstrækning er bestemt ved et naturligt rumkvantetal multipliceret med den fysiske elementarlængde, givet ved ligning (2). At det kosmiske rum kvantetal er lig med N³ er min opdagelse.

M₀ som jeg kalder universets totale energi-/stof masse spiller rollen som en øvre begrænsende størrelse, der sætter grænser for inertielle og gravitationelle virkninger og som ligeledes er bestemmende for det totale energiindhold i universet. M₀ er en meget fundamental størrelse og danner sammen med elementarlængden og en defineret elementartid det fysiske grundlag i min holistiske kvantekosmologi. Grundlæggende gælder: Enhver fysisk afstand er lig med et naturligt tal - rum kvantetallet - multipliceret med elementarlængden, ethvert fysisk tidsinterval er lig med et naturligt tal – tidskvantetallet – multipliceret med elementartiden og enhver masse er lig med en hel brøkdel af universets totale masse, eller et naturligt tal - massekvantetallet - multipliceret med elementarmassen.

N angiver som nævnt det aktuelle brøkforhold mellem de elektrostatiske- og de gravitostatiske kræfter mellem to elektroner, men N kan også opfattes som forholdet mellem størrelsen af det vi kunne kalde universets begyndelses gravitations-'konstant' G₀, og den aktuelle værdi af G i en bestemt kvantetilstand af universet. For voksende R , dvs. for et univers i udvidelse gælder, at G aftager. Af ligning (1) fås:

(3)

hvor

Af ligning (1) fås også:

(4)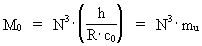

I ligning (4) angiver m_u en fysisk mindste massestørrelse - kvantemassen. Denne må være knyttet til eksistensen af det mindste energi-/stof kvantum i universet. Dette mindste energi/stof kvantum har jeg givet navnet en UNITON. Vi ser, at m_u svarer til en invariant, absolut og kosmologisk masse-enhed. Denne kosmiske masse-enhed betegner jeg med ordet 'masson'. Efterhånden som universet udvikler sig i kosmiske kvantespring - og R dermed forøges - vil antallet af unitoner vokse og dermed vil den kosmiske masseenhed formindskes. Af ligning (4) ses, at det aktuelle antal unitoner som universet består af, er lig med den aktuelle talværdi af det kosmiske evolutions kvantetal N³ .

I vor epoke er N³ = 7.2· 10¹²⁷ .

Vi ser, at én unitons masse er omvendt proportional med det aktuelle antal unitoner i universet.

Den gennemsnitlige unitontæthed n_u,cos - dvs. antal unitoner pr.rumfangsenhed - i universet er, bortset fra en geometrisk talfaktor, omtrentligt givet ved:

(5)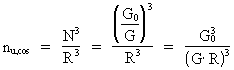

Med en udstrækning af universet på R = 10²⁶ m gælder i vor epoke, at n_{u,cos ,} er af størrelsesordenen 7· 10⁴⁹ unitoner pr. m³

Af ligning (5) ser vi, at unitontætheden i universet er stadigt aftagende (hvis universet udvider sig!), selv om antallet af unitoner er stadigt voksende.

Af ligning (1) fås for tilvæksten D (N³) af unitoner:

(6)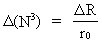

hvor D R er en kvantiseret tilvækst af universets udstrækning. For hvert kosmisk kvantespring, svarende til D R = r₀, dannes der én ny uniton. De nye unitoner må formodes at blive dannet på grænsen mellem det eksisterende univers og et kommende større univers.

En vis brøkdel - sandsynligvis svarende til N² elektroner - af universets unitoner er Bose-Einstein kondenseret i det vi kalder 'stof' og som på et højere kvanteniveau forefindes i form af elektroner, protoner og neutroner.

Af ligningerne (1) og (4) kan udledes en formel der viser, hvordan en unitons masse aftager efterhånden som universet udvider sig.

Lad os betragte to kvantetilstande af universet kendetegnet ved en udstrækning R₁ = n₁·r₀ og en udstrækning R₂ = n₂·r₀ , hvor n₂>n₁ er to kosmiske evolutionskvantetal . De hertil hørende unitonmasser betegnes m_u,₁ og m_u,₂

Følgende sammenhæng gælder:

(7)

For ét kosmisk kvantespring gælder n₂ = n₁+1 og vi kan skrive tilvæksten i unitonmasse D m_u som:

(8)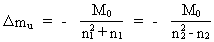

Af udtrykket i (8) ses, at den negative tilvækst i unitonmasse (svarende til at unitonmassen aftager) bliver mindre og mindre, efterhånden som det kosmiske evolutionskvantetal vokser.

I vor epoke hvor det kosmiske evolutionskvantetal er nået op på et uhyre stort tal, aftager unitonmassen uhyre lidt.

Et vigtigt spørgsmål: Hvad er det fysiske indhold af ligning (8)? Da unitonmassens aftagen bliver mindre og mindre efterhånden som universet udvikler sig, kan dette ikke umiddelbart forklares ved en simpel 'stofdeling' af lokalt eksisterende unitoner.

Derimod kan den aftagende unitonmasse være et mål for en aftagende inertiel masse og hvis dette er tilfældet må det betyde, at den inertielle egenskab ved stof ikke er en indre egenskab ved stoffet, men derimod bestemt af ydre kraftvirkninger. Spørgsmålet er da: Hvorfra kommer disse kraftvirkninger, der forsøger at forhindre accelerationen af et legeme? Svaret må være: De inertielle kraftvirkninger forårsages af unitonerne i det kosmiske uniton-felt!

Machs princip. Det kosmo-holistiske princip.

Siden mekanikkens tidligste barndom er der blevet tænkt over de såkaldte fiktive kræfter, også kaldet systemkræfter, idet de giver sig til kende i accelererede systemer. Eksempler på disse systemkræfter - der også betegnes inerti-kræfter - er: Centrifugalkræfter og corioliskræfter. Et spørgsmål, der er blevet stillet: Er disse kræfter fiktive, dvs. 'indbildte' eller er de reelle fysiske kræfter, der forårsages af fysiske systemer?

Spørgsmålet er specielt taget op af Isaac Newton (1642-1727), George Berkeley (1685-1753), Ernst Waldfried Josef Wenzel Mach (1838-1916) og Albert Einstein (1879-1955). Problemstillingen kan illustreres som følger:

Betragt en kugle, der roterer i forhold til resten af universets stoffordeling. Erfaringen viser, at kuglen vil bule ud ved de ækvatoriale områder. Spørgsmålet er: Hvorfor buler kuglen ud? Newton svarede: Kuglen buler ud, fordi den roterer i forhold til det absolutte rum. Er kuglen i hvile i forhold til det absolutte rum, vil den ikke bule ud, svarede Newton. Mach derimod sagde, at der er tale om en relativ effekt, der lige så vel ville opstå, hvis det var hele universet, der roterede i forhold til kuglen. Newton og Mach var således ikke enige. Ernst Mach analyserede egenskaberne inerti og gravitation i sin bog 'Die Mechanik' fra 1883. Einstein gik ind for Machs opfattelse og søgte at inkorporere hvad han kaldte 'Machs princip' i sin generelle relativitetsteori, men dette er dog ikke lykkedes entydigt.

Machs princip kan formuleres således:

Jeg vil formulere et helt generelt princip, 'Det kosmo-holistiske princip' :

Alt er bestemt af alt - Omnia determinant omnia.

Af ligning (3) og (4) fås følgende sammenhæng:

(9)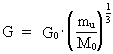

Ligning (9) giver en sammenhæng mellem gravitation - bestemt ved G og størrelsen en unitons masse bestemt ved m_u . Ligning (9) indeholder også universets totale masse M₀ og er således i overensstemmelse med 'Machs princip', der jo 'siger', at lokale inertielle og gravitationelle virkninger er bestemt af den samlede massefordeling i universet.

Vi ser af (9), at både gravitationskræfterne og inertikræfterne aftager efterhånden som universet i kosmiske kvantespring forøges i udstrækning! Det bemærkes, at de fundne relationer om universet alle er indeholdt i den 'kosmo-holistiske formel'!

Ved omformning af ligning (9) kan unitonmassen udtrykkes ved den aftagende gravitationelle størrelse G:

(10)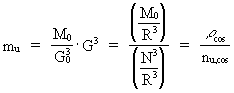

I ligning (10) angiver r _cos universets gennemsnitlige massefylde og n_u,_cos det gennemsnitlige antal unitoner pr. rumfangsenhed. Vi ser, at det jeg betegner som massen af en uniton er bestemt af masse- og unitonfordelingen i universet, altså i overensstemmelse med Machs princip.

Med eksistensen af det kosmiske uniton-hav kan såvel gravitationskræfter og inertikræfter såsom centrifugal -og corioliskræfter forklares som forårsaget af unitonvekselvirkninger mellem et givet legemes unitoner og unitonerne i det kosmiske uniton-hav.

Nogle fysikfundamentale spørgsmål:

• Hvad er masse et mål for, og hvordan defineres den?
• Haves en entydig definition?
• Angiver massestørrelsen en naturgiven indre egenskab ved stoffet?
• Eller er det en størrelse vi har indført i mangel af en dybere forståelse for de virkelige forhold og dermed af praktiske grunde?

Det sidste spørgsmål vil jeg besvare med et ja, og de to næstsidste med et nej. Jeg mener, at stof ikke er i besiddelse af indre egenskaber der svarer til de massestørrelsen man definerer i fysikken. I den etablerede fysik opereres der i det væsentlige med tre massedefinitioner, nemlig: 1) Den inertielle masse, 2) den aktive gravitationelle masse og 3) den passive gravitationelle masse. De tre massestørrelser er mål for og defineret ved følgende:

Den inertielle masse af et afgrænset stofsystem - et legeme - er et mål for den inerti. træghed eller modstand som legemet 'udviser' når det bliver accelereret, dvs. får en hastighedsændring, målt i forhold til et givet referencesystem. Et legemes inertielle masse er defineret som en proportionalitetskonstant i Newtons 2.lov:

(11)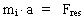

m_i er størrelsen af legemets inertielle masse, a størrelsen af den acceleration der forårsages af en resulterende kraft af størrelsen F_res.

Den aktive gravitationelle masse er defineret som et mål for størrelsen af det aktive gravitationsfelt der eksisterer omkring en given stoffordeling. Den passive gravitationelle masse af en 'partikel' (der ikke forstyrrer det aktive gravitationsfelt væsentligt) er et mål for størrelsen af den gravitationskraft som partiklen bliver påvirket af, når denne befinder sig i et aktivt gravitationsfelt.

En yderst vigtig eksperimentel erkendelse er: Den inertielle masse af en afgrænset stofportion er ligefrem proportional med samme stofportions gravitationelle masse, i passende enheder - eksempelvis kg - har de samme talværdi. Denne lighed mellem inerti og gravitation blev stærkt fremhævet af Isaac Newton (1642-1727). Newton efterprøvede ligheden ved svingningsforsøg med penduler, hvor pendullegemerne var af forskellige stoffer. Mere nøjagtige forsøg blev udført i slutningen 1890'erne af den ungarske forsker Roland von Eötvös (1848-1919). Von Eötvös benyttede en torsionsvægt som han oprindelig havde udviklet til måling af lokale variationer i tyngdekraften. Også nyere og meget mere følsomt apparatur har påvist en identitet mellem inertiel og gravitationel masse. Denne identitet mellem inertiel og gravitationel masse tyder på en intim sammenhæng mellem inertielle og gravitationelle virkninger. At der er lighed mellem inertiel og gravitationel masse formuleres i det såkaldte 'ækvivalensprincipt'. Ækvivalensprincippet der danner grundlaget for Einsteins generelle relativitetsteori kan kort formuleres på følgende måde:

Et kinematisk accelerations-felt er ækvivalent med et stoffremkaldt gravitations-felt.

Ifølge Einsteins generelle relativitetsteori skulle det være umuligt ved noget fysisk eksperiment at påvise en forskel mellem et 'kinematisk gravitations-felt' og et 'stofligt gravitations-felt'.

Ifølge min 'Maxwell-analoge gravitationsteori med to gravitationsfelter' (se denne) er der en umiddelbar feltmæssig forskel på et 'kinematisk gravitationsfelt' og et 'stofligt gravitationsfelt'. Denne forskel giver en eksperimentel mulighed for at afgøre i mellem de to tilfælde. Men når man analyserer kraftvirkningerne på det fundamentale uniton-mekaniske niveau, træder lighederne frem, idet både gravitationskræfter og inertikræfter forårsages af uniton-vekselvirkninger!

Gravitationskræfter og inertikræfter (og for den sags skyld alle kraftvirkninger) er et resultat af vekselvirkninger mellem unitoner og kræfternes størrelser har med bl.a. antal vekselvirkende unitoner at gøre. Da antallet af vekselvirkende unitoner er afgørende for de observerede kraftvirkninger mellem systemerne er det hensigtsmæssigt med en fysisk massestørrelse der er defineret som et antalsmål for unitoner. Lad os derfor definere følgende kosmiske massestørrelse baseret på et bestemt antal unitoner:

Omvendt skal der ved en afgrænset stofportion - et legeme - forstås et område med et bestemt antal unitoner.

Den herved definerede kosmiske massestørrelse er en kosmisk invariant størrelse som i princippet blot kræver en tælling af antal unitoner. Andre intelligensvæsner i universet vil også kunne bestemme en given stofportions kosmiske masse ved - i princippet - en tælleproces!

Lad os definere et legemes kosmiske masse m ved:

(12)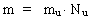

hvor m_u er en proportionalitetsfaktor der defineres som én unitons kosmiske masse og som kan vælges at have enheden kg. N_u er antal unitoner som legemet består af.

I kosmologiske enheder, hvor m_u vælges som masseenhed - en masson - er talværdien af m lig med antallet af unitoner som et givent legeme består af. I kosmologiske enheder bestemmes et legemes masse ved en optælling af antal unitoner og massemåling er således blevet til en tælleproces!.

Ved benyttelse af (10) kan massen m udtrykkes ved M₀, G₀ og G eller ved universets massetæthed og unitontæthed:

(13)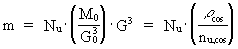

Af udtrykket i (13) ser vi, at et legemes inerti afhænger af massetætheden - og unitontætheden i universet. Dette er helt i overensstemmelse med Machs princip. Vi ser, at dette også gælder for G.

Begrebet 'tid' er blevet analyseret af mange tænkere, specielt filosoffer. Disse er dog ikke nået til enighed om en entydig definition af begrebet. Selv om 'tidsstørrelsen' spiller en fundamental rolle i beskrivelsen af fysiske fænomener, nemlig som en ' løbende uafhængig variabel', er det kun meget få fysikere der har beskæftiget sig med det fundamentale 'tidsbegreb'. Så vidt jeg kan se, er problemet af definitionsmæssig karakter, idet det er vigtigt at definere et hvilket som helst begreb, betegnet med et specifikt ord, så entydigt som muligt. Et bestemt begreb, angivet ved et bestemt ord, bør ikke have forskellige betydninger, slet ikke hvis det er et begreb der benyttes i naturvidenskabelige studier. Hvis et overordnet begreb som 'tid' gives flere betydninger, da bør det deles op i 'delbegreber' betegnet med hvert sit specifikke ord eller valg af flere ord. Man kan således definere og tale om: 'Fysisk tid', (dvs. 'naturtid'), 'biologisk tid', 'psykologisk tid' , 'historisk tid' osv. Med hensyn til 'fysisk tid' kan denne med fordel deles op i: 'Lokal fysisk tid' og 'kosmisk fysisk tid'. For at kunne sammenligne disse to tidsmål må der eksistere en sammenhæng mellem dem. Det 'kosmiske tidsmål' som jeg her vil definere er en invariant og absolut størrelse, hvorimod en defineret 'lokal fysisk tid' er en relativ størrelse.

Vi kan spørge:

• Hvad skal vi forstå ved 'fysisk tid'?
• Hvordan kan vi definere begrebet 'fysisk tid' entydigt?
• Kan et invariant og absolut kosmisk tidsmål defineres?

Jeg vil definere begrebet 'tid' på følgende måde:

Med et motto på latin kan vi udtrykke: 'TEMPUS MUTATIO EST'

Da der forekommer mange slags forandringer i naturen er spørgsmålet: Hvilke forandringsprocesser skal vi vælge til en tidsdefinition? Med ovenstående viden om et stadigt diskret voksende univers kan et kosmisk fysisk tidsinterval D T defineres således:

eller:

(14)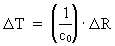

hvor vi - af enhedsmæssige grunde - har valgt reciprokværdien af lysets hastighed c₀ som proportionalitetskonstant. Talværdien af lysets hastighed er målt i forhold til et lokalt defineret tidsmål. Da den mindste tilvækst af D R = r₀ dvs. lig med den fysiske elementarlængde, ser vi, at dette svarer til et mindste tidsinterval t₀ - elementartiden givet ved:

(15)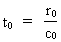

Ved benyttelse af ligning (6) kan vi også skrive (12) som:

(16)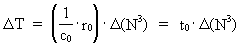

Af ligning (16) ser vi, at D T = t₀ for D (N³) = 1 , dvs. der dannes én ny uniton for ethvert kvantetidsinterval der er lig med elementartiden, og svarende til ét kosmisk kvantespring.

Elementartiden definerer en invariant og absolut kosmologisk tidsenhed som jeg betegner en tempon . Da det nuværende univers består af 7.2× 10¹²⁷ unitoner, dvs. at der indtil vor epoke er blevet dannet dette antal unitoner, svarer dette til en alder af universet på 7.2× 10¹²⁷ temponer.

Universets aktuelle alder T er således ligefrem proportional med det aktuelle antal unitoner N³. Elementartiden spiller rollen som en proportionalitetskonstant. Der gælder således:

(17)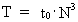

Universets absolutte alder kan således - i princippet - bestemmes ved en 'tælleproces'!

Sammenhængen i ligning (17) giver løsningen på det man kalder 'tidens pil', dvs. det forhold, at begivenhederne i universet altid forløber i en bestemt retning. Begivenhedernes retning er åbenbart i den retning, hvor antallet af unitoner i universet er voksende!

Universets aktuelle udstrækning R er også bestemt af antal unitoner, og i det hele taget er alt i universet bestemt ved antallet af unitoner! Man kunne sige: 'Tæl, og du vil vide'!.

Der eksisterer følgende sammenhæng mellem universets alder og den aktuelle masse af én uniton:

(18)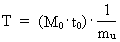

Af ligning (18) ser vi, at universet aktuelle alder er omvendt proportional med den aktuelle masse af én uniton. 'Kosmisk fysisk tid' kan således siges at være ækvivalent med unitonmassen!

  Næste artikel