|
Universets mindsteværdier af impuls, impulsmoment og energi
Af Louis Nielsen Indledning I det følgende vil jeg foretage en generel rationel kvantisering af nogle af de fysiske størrelser og formeludtryk, der indgår i den klassiske mekanik. Den generelle kvantisering er en direkte konsekvens af rummets, tidens og massens basiskvantisering. Eksistensen af denne basiskvantisering - og de kosmologiske konsekvenser heraf - har jeg redegjort for i min holistiske kvantekosmologi. Grundlaget for det følgende - og min holistiske kvantekosmologi - er eksistensen af følgende kvantekosmologiske fundamentalstørrelser:
De kosmologiske kvantestørrelser definerer et absolut og
kosmologisk enhedssystem, der er uafhængigt af specifikke
lokalsystemer og levende systemers eksistens.
(Se afsnit 5 i min afhandling).
Som en konsekvens af de fysiske størrelsers kvantisering vil alle lovmæssigheder og formelsammenhænge i vor naturbeskrivelse være kvantiserede, dvs. at der i formlerne indgår karakteristiske rationelle kvantetal. Naturlovene vil som følge heraf kunne formuleres som kvantetalsbetingelser. Betegnelsen holistisk refererer til det faktum, at der i de fysiske udtryk indgår størrelser fra såvel mikrokosmos – eksempelvis Plancks konstant og en unitons masse – og størrelser fra makrokosmos – eksempelvis universets totale masse. Som følge af de grundlæggende fysiske størrelsers
basiskvantisering bør alle naturfænomener – fundamentalt betragtet -
beskrives ved en diskret matematik og ikke, som det har været
praktiseret siden Newton, ved en kontinuert matematik. Da elementarlængden
og den dertil hørende elementartid er uhyre små størrelser -
når de angives ved vore praktiske måleenheder – kan dagligdags og
makroskopiske fænomener stadig med fordel og stor nøjagtighed
beskrives ved hjælp af en kontinuert matematik. Hvis man derimod
ønsker en korrekt beskrivelse og forståelse af mikrofysiske
fænomener og de allertidligste stadier af universets udvikling, da
må en diskontinuert matematik benyttes. I et tidligere kapitel har jeg
overvejet nogle konsekvenser, af det jeg kalder en fysisk kvantegeometri.
Med eksistensen af en mindste fysisk ’afstandsmålestok’ kan vi ikke i en
forfinet beskrivelse af naturen benytte den euklidisk kontinuerte geometri.
I en fysisk kvantegeometri, må vi kvantisere de geometriske
afstandsdimensioner af eksempelvis en ’cirkel’ således, at forholdet
mellem kvantecirklens ’kvanteomkreds’ og ’kvantediameter’ definerer et
rationelt pi, Jeg viser, at det maximale arbejde, der blev udført i universet, da dette blev født i løbet af det første kosmiske kvantetidsinterval, er givet ved universets totale masse multipliceret med lysets fart i anden potens. Størrelsen af dette maximale arbejde er lig med den totale energi, der opstod i universet, da dette foretog sit første kosmiske kvantespring over elementarlængden! Ved anvendelse af min kvantekosmologiske ligning, der forbinder universets totale masse med en unitons masse, kan jeg på en simpel måde udlede den berømte formel E = m·c02 , hvor m er et systems masse og c0 er lysets fart. I det følgende vil jeg betragte nogle specielle systemers kvanteforhold, bl.a. kvantebevægelsen af en partikel, der bevæger sig i et homogent tyngdefelt. Jeg viser, at energien af en partikel eller et givet system enten kan angives som en rationel brøkdel af universets totale energi, eller som et helt multiplum af en unitons kinetiske energi.
Rummets, tidens og massens kvantisering. Kvantekinematik og kvantedynamik Den fysisk mindste afstand i universet - elementarlængden r0 og det fysisk mindste tidsinterval - elementartiden t0 er givet ved: (1) 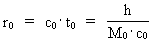 hvor h er Plancks konstant, M0 universets totale energi-/stof-masse og c0 lyskonstanten. Enhver endelig fysisk afstand (2) 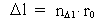 hvor Ethvert endeligt fysisk tidsinterval (3) 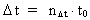 hvor Som en naturlig konsekvens af (2) og (3) vil også de fysiske størrelser hastighed og acceleration være kvantiserede størrelser. For en partikel, der bevæger sig i et givet referencesystem, definerer vi den kvantiserede hastighed v – langs med en bestemt retning - som en tilbagelagt strækning divideret med det tilhørende tidsinterval. Ved benyttelse af de basiskvantiserede størrelser i (2) og (3) fås da for v: (4) 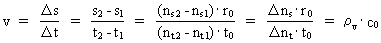 hvor (5) 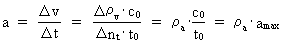 hvor For ethvert system med en masse m antages, at denne er en rationel brøkdel af universets totale masse M0, dvs.: (6) 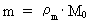 hvor I et givet referencesystem vil vi definere en partikels kvantiserede impuls p – i en bestemt retning - ved følgende: (7) 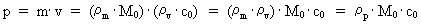 hvor
Kvantekraft og kvantearbejde Hvis en partikel i et givet referencesystem accelererer, dvs. ændrer hastighed, da siger vi, at partiklen er påvirket af en eller flere kræfter. Størrelsen Fres af den samlede kraftpåvirkning på partiklen, også kaldet den resulterende kraft, defineres som ændringen i partiklens impuls divideret med det hertil hørende tidsinterval, dvs. således: (8) 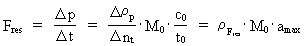 I ligning (8) er En konstant krafts arbejde AF over en strækning
(9) 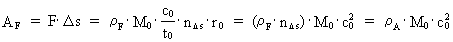
Størrelsen M0·c02 angiver – som jeg vil vise i det følgende - den totale energi i universet! Ethvert subsystems energiindhold er således lig med en rationel brøkdel af universets totale energi! Et udført arbejde på et system er ensbetydende med en
energiudveksling mellem de kraftudvekslende systemer. Størrelsen af det
arbejde Ares, den resulterende kraft udfører på
en partikel, er lig med partiklens tilvækst i kinetisk energi
(10) 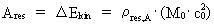
Universets embryonale arbejde og dets totale energiindhold Da universet blev ’født’ og foretog sit første kosmiske kvantespring over en afstand lig med elementarlængden, ’opstod’ den totale energi, som eksisterer i universet. Denne totale energi er siden blevet fordelt som kinetisk energi hos alle de mindste stof-/energikvanter – unitoner – som alt i universet består af. Vi kan beregne denne totale kosmiske energi Ekin,cos ved at udregne det fysisk maximale arbejde Amax, der blev udvirket over elementarlængden r0: (11) 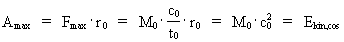 Vi ser, at universets totale energi er bestemt ved produktet af dets totale masse og lysets fart i anden potens, altså et beregningsudtryk, der svarer til det, Albert Einstein fandt frem til i sin specielle relativitetsteori fra 1905. Her er jeg dog kommet til udtrykket på en kvantefysisk og dermed fundamentalt anden måde!
Udledning af formlen E = m·c02 og en uniton-mekanisk forklaring I min holistiske kvantekosmologi (se denne) viser jeg eksistensen af følgende sammenhæng: (12) 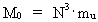 hvor N3 er det kosmiske evolutionskvantetal, der styrer universets udvikling og er en diskret parameter, der ’tikker’ op gennem de naturlige tal. N er lig med det aktuelle brøkforhold mellem de elektrostatiske og gravitostatiske kræfter mellem to elektroner. mu er massen af en uniton. Af (12) ser vi, at der i enhver tilstand af universet eksisterer N3 unitoner. I vor epoke er N3 = 7,2·10127 svarende til et uhyre stort antal unitoner. Enhver afgrænset stofmængde består af et bestemt antal unitoner. Ved indsættelse af udtrykket i (12) i ligning (11) får vi: (13) 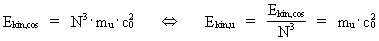 Af lignig (13) ser vi at den kinetiske energi af en uniton
Ekin,u er bestemt ved produktet af unitonens masse og lysets fart i
anden potens! Denne unitonkinetiske energi er den fysisk mindste
energimængde – elementarenergien - i det aktuelle univers. (14) 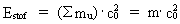 Det totale energiindhold Estof af en bestemt
stofmængde er således givet ved produktet af stofmængdens
masse og lysets fart i anden potens!
Universets mindsteværdier af impuls, impulsmoment og energi Ved at anvende sammenhængen i ligning (12) kan vi udtrykke forskellige systemers energiindhold som et helt multiplum af én unitons kinetiske energi. Ved en partikel vil vi forstå et afgrænset unitondynamisk system, der består af et bestemt antal unitoner. Partiklens unitondefinerede masse m er givet ved: (15) 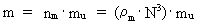 hvor nm er et naturligt tal - massekvantetallet.
(16) 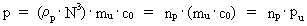 hvor np er et naturligt tal – det naturlige impulskvantetal.
(17) 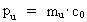 angiver den mindste fysiske impuls – elementarimpulsen - i universet. Hvis denne elementarimpuls multipliceres med universets udstrækning R, fås den fysiske størrelse, som kaldes et impulsmoment. Produktet af pu og R giver Plancks konstant h, dvs. der gælder: (18) 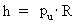 Det ses, at Plancks konstant ikke er så fundamental, som man formoder i den kendte fysik, idet elementarimpulsen og universets udstrækning må opfattes som mere fundamentale! Udtrykket i (18) er i øvrigt et grænsetilfælde af Heisenbergs usikkerhedsrelation for impuls og sted, idet den angiver sammenhængen mellem minimumusikkerhed på impuls og maximumusikkerhed på sted. Ved at indføre elementarlængden r0 i (18) kan vi finde talværdien af det fysisk mindste impulsmoment i universet – elementarimpulsmomentet lu: (19) 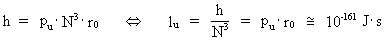 Vi ser, at talværdien af elementarimpulsmomentet er uhyre lille angivet
i de af os definerede SI-enheder. Hvis vi derimod angiver elementarimpulsmomentet
i de kosmologiske enheder, da er talværdien lig med 1 med
enheden (masson·spaton²)/tempon. (20) 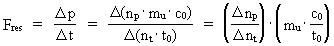 hvor Ligningerne (10) og (11) kan omformes til: (21) 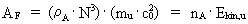 (22) 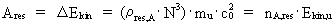 hvor nA og nA,res kan opfattes som naturlige
arbejdskvantetal. Ekin,u er én unitons kinetiske
energi, og denne er den fysisk mindste energistørrelse i
universet – elementarenergien. I kosmologiske enheder er talværdien
af elementarenergien lig med 1.
(23) 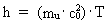 altså som produktet mellem elementarenergien og universets alder. Ligning (23) er ligesom udtrykket i (18) et grænsetilfælde af Heisenbergs usikkerhedsrelation for tid og energi. En partikels kvantebevægelse i et homogent tyngdefelt Lad os analysere energiforholdene af en partikel, der bevæger sig i et homogent tyngdefelt, idet vi gør brug af de kvantiserede energiudtryk. Den kinetiske energi Ekin af en partikel kan skrives: (24) 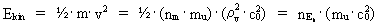 hvor m er partiklens masse, der er lig med et naturligt tal gange en unitons
masse. v er den rationelt kvantiserede hastighed, og nEk er
et naturligt tal – det kinetiske energikvantetal. Af (24) ser
vi, at partiklens kinetiske energi er givet ved et helt multiplum af
elementarenergien.
(25) 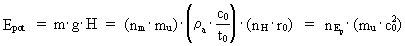 hvor g er stedets tyngdeacceleration, der er lig med et rationelt accelerationskvantetal multipliceret med den universelle maximalacceleration – forholdet mellem lysfarten og elementartiden. H er den lodrette højde målt fra et valgt nulniveau og bestemt ved et rumkvantetal ganget med elementarlængden. nEp er energikvantetallet hørende til den potentielle energi – det potentielle energikvantetal. Vi ser af (25), at også den tyngdepotentielle energi kan beregnes som et helt multiplum af elementarenergien. En partikel, der bevæger sig i det homogene tyngdefelt, har inden for ethvert kvantetidsinterval en total såkaldt mekanisk energi Emek givet ved: (26) 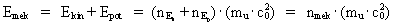 hvor nmek er det mekaniske energikvantetal.
(27)  Under partiklens bevægelse gælder der således: (28) 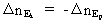 Udtrykt i ord betyder ligning (28): Lige så meget som det kinetiske energikvantetal stiger, lige så meget falder det potentielle energikvantetal! Hvis eksempelvis det potentielle energikvantetal falder med 10, da vil det kinetiske energikvantetal stige med 10. I praksis vil talændringerne være uhyre store. Men fundamentalt betragtet må det formodes, at naturen fungerer sådan, som jeg har beskrevet!
© Louis Nielsen, 5. juli 1998
|
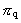 Ligeledes vil den
pythagoræiske læresætning ikke være gyldig i en fysisk
kvantegeometri.
Ligeledes vil den
pythagoræiske læresætning ikke være gyldig i en fysisk
kvantegeometri.
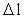 er givet ved:
er givet ved:
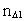 er et naturligt tal - rumkvantetallet.
er et naturligt tal - rumkvantetallet.
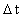 er givet ved:
er givet ved:
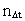 er et naturligt tal – tidskvantetallet.
er et naturligt tal – tidskvantetallet.
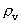 er et rationelt hastighedskvantetal, der kan antage rationelle
talværdier mellem 0 og 1.
er et rationelt hastighedskvantetal, der kan antage rationelle
talværdier mellem 0 og 1.
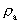 er et rationelt accelerationskvantetal, der kan antage rationelle
talværdier mellem 0 og 1. amax er lig med forholdet
mellem lyshastigheden og elementartiden og er som sådan en maximal
øvre fysisk acceleration i universet. Den maximale acceleration forekom,
da universet med dets stof og bevægelser blev ’født’ ved det
første kosmiske kvantespring over en afstand lig med elementarlængden!
er et rationelt accelerationskvantetal, der kan antage rationelle
talværdier mellem 0 og 1. amax er lig med forholdet
mellem lyshastigheden og elementartiden og er som sådan en maximal
øvre fysisk acceleration i universet. Den maximale acceleration forekom,
da universet med dets stof og bevægelser blev ’født’ ved det
første kosmiske kvantespring over en afstand lig med elementarlængden!
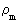 kan kaldes det kosmiske massekvantetal.
kan kaldes det kosmiske massekvantetal.
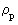 er det rationelle impulskvantetal, der kan antage rationelle
talværdier mellem 0 og 1.
er det rationelle impulskvantetal, der kan antage rationelle
talværdier mellem 0 og 1.
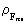 et rationelt kraftkvantetal, der kan antage rationelle talværdier
mellem 0 og 1.
et rationelt kraftkvantetal, der kan antage rationelle talværdier
mellem 0 og 1.
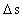 defineres - hvis kraftretning og forskydningsretning er parallelle – som:
defineres - hvis kraftretning og forskydningsretning er parallelle – som:
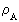 definerer et rationelt arbejdskvantetal, eller energikvantetal,
der kan antage rationelle talværdier mellem 0 og 1.
definerer et rationelt arbejdskvantetal, eller energikvantetal,
der kan antage rationelle talværdier mellem 0 og 1.
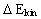 Af (9) får vi for den resulterende krafts arbejde:
Af (9) får vi for den resulterende krafts arbejde:
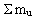 af masserne af de unitoner, som stofmængden består af, gælder:
af masserne af de unitoner, som stofmængden består af, gælder:
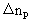 og
og 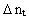 angiver de samhørende tilvækster i henholdsvis impulskvantetal
og tidskvantetal.
angiver de samhørende tilvækster i henholdsvis impulskvantetal
og tidskvantetal.