|
Fundamentale kvantekosmologiske enheder og universets kvanteudvikling
Af lektor, cand. scient. Louis Nielsen
Herlufsholm, Næstved
Indledning
I det følgende vil jeg vise, at der i vort univers eksisterer et absolut og kosmologisk enhedssystem, der er uafhængigt af levende væsener og specifikke lokalsystemer.
I min holistiske kvantekosmologi – der kan studeres andetsteds – har jeg baseret de teoretiske udledninger på eksistensen af en fysisk mindste afstand – elementarlængden, et fysisk mindste tidsinterval – elementartiden og universets totale
stof-/energimasse. Min opdagelse af en sammenhæng mellem universets totale masse, elementarlængden, elementartiden og Plancks »konstant« og lyskonstanten giver en holistisk sammenhæng i vort univers. Der eksisterer en sammenhæng mellem mikrokosmos og makrokosmos. Da universets mindste fysiske afstand er bestemt af universets totale masse, kan man også udtrykke det sådan: »Det største er indeholdt i det mindste!«.
I min holistiske kvantekosmologi vises det, hvilke sammenhænge der er mellem
universets aktuelle udstrækning, universets alder (den kosmiske tidsparameter)
og elementarlængden og elementartiden. Ligeledes gives en sammenhæng
mellem universets totale masse og den til enhver tid mindste fysiske masse i vort
univers – elementarmassen. Universet har udviklet sig fra ét kvantum
– den kosmiske embryoton. Den kosmiske embryoton havde en udstrækning
lig med elementarlængden, og universet – rum og tid, og dermed
naturlovene – blev dannet inden for det første kosmiske kvantetidsinterval.
Universets udvikling »styres« af et kosmisk evolutionskvantetal,
der »tikker« op igennem de naturlige tal.
Universet blev »født«, da dette evolutionskvantetal antog
værdien én! »I dag« er dette kosmiske kvantetal nået
op på det uhyre store tal 7,2 · 10127.
Universets udvikling kendetegnes ved, at den oprindelige kosmiske embryoton deles op i
flere og flere elementarkvanter. Det aktuelle antal af disse elementarkvanter er
lig med det kosmiske evolutionskvantetal.
Opdelingen og spredningen af den energi, der oprindelig var koncentreret i den
kosmiske embryoton, er i overensstemmelse med entropiloven, der
»kræver«, at et system udvikler sig fra en mindre sandsynlig
og tæt tilstand til en mere sandsynlig og mindre tæt tilstand.
Da universet udvikler sig fra én kvantemasse til flere og flere kvantemasser,
der spredes i det ekspanderende rum, vil dette have som konsekvens, at den
kosmologiske masseenhed varierer, efterhånden som universet udvikler sig!
Denne kosmiske variation af den fysiske grundenhed for masse vil have meget
interessante følger for de fysiske størrelser, vi har defineret for
at kunne beskrive det univers, vi selv er en del af. Som det vil blive vist i det
følgende, kan universets udvikling karakteriseres som en udvikling op
igennem de naturlige tal! Angivet i kosmologiske enheder vil
mange af de fysiske størrelser, som vi formoder er konstante, vise
sig ikke at være konstante; dette gælder eksempelvis
Plancks »konstant«.
Fysiske størrelser og deres enheder
For at kunne beskrive fænomenerne i det univers, vi selv er en del af, har vi defineret forskellige fysiske størrelser. En fysisk størrelse er karakteriseret ved et matematisk tal, en enhed og evt. en retning. Vor oplevelse af et tilsyneladende lovmæssigt fungerende univers er bl.a. begrundet i den opdagelse, at der mellem bestemte fysiske størrelser eksisterer en matematisk sammenhæng, ofte en ret simpel sammenhæng.
Det har vist sig, at alle fysiske størrelser kan defineres ud fra nogle få fundamentale fysiske størrelser.
Selv om vi har flere muligheder for valget af fysiske fundamentalstørrelser, tyder meget på, at universet »selv« har bestemt, hvilke grundstørrelser andre fysiske størrelser skal udledes fra. Disse fundamentale størrelser er:
- Rumlig afstand mellem to »punkter«
- Tidsligt interval mellem to begivenheder
og
- Masse af et stof-/energiholdigt system
For at kunne angive bestemte afstande, tidsintervaller og masser er det nødvendigt – også for at kunne kommunikere størrelserne med andre mennesker – at vedtage enheder for afstand, tidsinterval og masse. Vi har utallige muligheder for valget af enhedernes definitioner, men det meget interessante og vigtige spørgsmål er: Eksisterer der et universelt og absolut enhedssystem, der er uafhængigt af levende væsener og specifikke lokalsystemer? Det stillede spørgsmål vil jeg besvare med et: Ja! Et ja, idet jeg mener at have opdaget disse absolutte kosmologiske fundamentalenheder!
Vi skal komme tilbage til disse kosmologiske enheder, men først gøre et par bemærkninger om de måleenheder, vi normalt benytter i vor fysiske beskrivelse af omverdenen. Næsten alle lande er blevet enige om at benytte de samme fysiske enheder. Disse er: afstandsenheden meter, tidsenheden sekund og masseenheden kilogram. Før i tiden var der et sandt kaos med hensyn til grundenheder, idet man benyttede forskellige enheder i forskellige lande; ja endog inden for det samme land kunne man benytte forskellige enheder.
De i dag benyttede grundenheder, meter, kilogram og sekund er dog langt fra at være kosmologiske; derimod har de en oprindelse, der er tæt forbundet til et menneskes dimensioner og rytmer. En meter svarer nogenlunde til længden af et ben hos et voksent menneske. Et sekund svarer nogenlunde til intervallet mellem to pulsslag, og et kilogram svarer omtrent til en tredjedel af et nyfødt barns vægt.
Efterhånden indså man, at det var fornuftigt at definere fysiske grundenheder uafhængigt af et menneskes relationer. Eksempelvis blev længdeenheden meter indført under den franske revolution, og i 1791 blev den defineret som en timilliontedel af afstanden fra Ækvator til Nordpolen, målt langs længdecirklen gennem Paris. På basis af gradmålinger fremstillede man en standard af platin, den såkaldte arkivmeter. Denne arkivmeter skulle da være en sekundær meternormal. Senere gradmålinger viste imidlertid, at arkivmeteren var omkring 2/10 mm kortere end 1/107 af jordkvadrantens længde. Derfor ophøjede man arkivmeteren tilprimær normal, idet en meter defineredes som afstanden mellem arkivmeterens plane endeflader ved en temperatur på 0° Celcius. Man gav således afkald på en forbindelse mellem meteren og naturobjektet Jorden. Sidenhen er meterenheden blevet justeret og omdefineret flere gange. På den 11. generalkonference for mål og vægt i Paris i 1960 vedtog man en ny meterdefinition. Denne meterdefinition var nu knyttet til en bestemt fotonstråling fra krypton-86 atomet. Man vedtog: En meter er lig med 1650763,73 gange bølgelængden i vacuum af den stråling, der svarer til overgangen mellem niveauerne 2 p10 og 5 d5 i atomer af krypton-86.
Stoney-»enheder« og Planck-»enheder«
På et møde i Belfast i 1874 fremlagde den irske fysiker George Johnstone Stoney (1826-1911) [G. Johnstone Stoney: 'On the Physical Units of Nature', Philosophical Magazine, 11,381 (1881).] et forslag til nogle »naturlige« enheder for længde, tid og masse, der var uafhængige af menneskets eksistens. Ved passende kombination af Newtons gravitationskonstant, lysets hastighed og en elektisk ladningsenhed, som Stoney selv havde foreslået og beregnet talværdien af, kunne han konstruere en længde, en tid og en masse. Stoney kom frem til følgende talværdier:
Længde = 10-37 meter, tid = 0,3 · 10-45 sekund og masse = 10-7 gram. Det bemærkes, at elektronen først blev opdaget i 1897, og at navnet »elektron« blev indført af Stoney i 1891 som betegnelse for den mindste elektrolytiske ladningsenhed. Det bemærkes ligedes, at Stoneys enheder er indført rent ad hoc uden tilknytning til nogen teori.
I 1899 gav Max Planck (1858-1947) [Max Planck: »Über irreversible Strahlungsvorgänge«. Sitzungsberichte der Preußischen Akademie der Wissenschaften, 5, 479 (1899)] en matematisk beskrivelse af den elektromagnetiske udstråling fra et »absolut sort legeme«. For at kunne redegøre for de eksperimentelle fakta måtte Planck bryde med den klassiske kontinuerte fysik, idet han måtte antage, at strålingen blev udsendt i diskrete energiportioner — kaldet kvanter. Energien af ét strålingskvantum var ligefrem proportional med frekvensen af en specifik stråling.
Proportionalitetskonstanten, der sammenknytter energien af et kvantum og frekvensen, definerer den konstant, vi i dag kalder Plancks konstant. Med kvantiseringen af strålingsenergien og indførelsen af Plancks konstant blev kvantefysiske betragtninger indført i beskrivelsen af naturen.
Efter indførelsen af sin kvantekonstant (Plancks konstant) viste Max Planck ved en ren dimensionsbetragtning, at man kunne konstruere en længde, en tid og en masse ved hjælp af Newtons gravitationskonstant, lysets hastighed og den nyindførte Planck-konstant. Beregningsformlerne for det, man i dag kalder Planck-længden lp, Planck-tiden tp og Planck-massen mp er givet ved:
(p1)
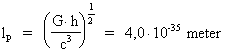 (p2)
(p2)
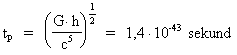 (p3)
(p3)
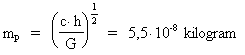 I disse formler er G Newtons gravitationskonstant, h Plancks konstant og c lysets hastighed.
I disse formler er G Newtons gravitationskonstant, h Plancks konstant og c lysets hastighed.
Ved at benytte Boltzmanns termodynamiske konstant k kunne Planck også konstruere en uhyre høj temperatur. Denne Planck-temperatur er givet ved:
(p4)
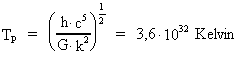 Størrelserne defineret ved udtrykkene (p1) til (p4) er konstrueret ad hoc uden sammenhæng med nogen teoridannelse, og Max Planck selv var meget imod en diskontinuert fysik.
Størrelserne defineret ved udtrykkene (p1) til (p4) er konstrueret ad hoc uden sammenhæng med nogen teoridannelse, og Max Planck selv var meget imod en diskontinuert fysik.
I dag benytter flere kosmologer disse Planckstørrelser som en tidlig tilstand af universet – dette til trods for, at størrelserne ikke kan begrundes som værende basis for en fysisk teori. Begrundelsen for deres benyttelse er deres lidenhed – noget meget mindre, som mine elementarstørrelser, har man svært ved at forestille sig.
Elementarlængden og elementartiden. Rummets og tidens kvantisering
Rumkvantet – elementarlængden r0 er givet ved:
(1) 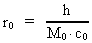 hvor h er Plancks konstant, M0 universets totale stof-/energimasse og c0 lysets hastighed i feltfrit vacuum, en størrelse, jeg vil kalde lyskonstanten.
hvor h er Plancks konstant, M0 universets totale stof-/energimasse og c0 lysets hastighed i feltfrit vacuum, en størrelse, jeg vil kalde lyskonstanten.
Tidskvantet – elementartiden t0 er givet ved:
(2) 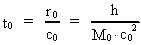 Massen af en »elementarpartikel« antages at være en bestemt brøkdel af universets totale masse. Eksempelvis gælder der for elektronens gravitationelle masse me:
Massen af en »elementarpartikel« antages at være en bestemt brøkdel af universets totale masse. Eksempelvis gælder der for elektronens gravitationelle masse me:
(3) 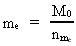 hvor jeg vil kalde nme for elektronens kosmiske massekvantetal, der er et uhyre stort tal.
hvor jeg vil kalde nme for elektronens kosmiske massekvantetal, der er et uhyre stort tal.
I en rationel kvantefysik gælder:
Enhver fysisk endelig afstand 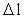 er lig med et naturligt tal – rumkvantetallet er lig med et naturligt tal – rumkvantetallet 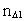 multipliceret med elementarlængden r0. Dvs. der gælder: multipliceret med elementarlængden r0. Dvs. der gælder:
(4) 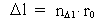 Ligeledes gælder: Ethvert fysisk tidsinterval
Ligeledes gælder: Ethvert fysisk tidsinterval 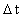 er lig med et naturligt tal – tidskvantetallet er lig med et naturligt tal – tidskvantetallet 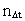 multipliceret med elementartiden t0. Dvs. der gælder: multipliceret med elementartiden t0. Dvs. der gælder:
(5) 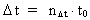 Alle fysiske størrelser, såsom hastighed, acceleration, kraft, arbejde, energi osv., defineres som sædvanligt, men vi må nu tage hensyn til kvantiseringen af rum, tid og masse. Denne fundamentale »atomisering« medfører, at al bevægelse er diskontinuert, — bevægelser foregår i »spring«. Ligeledes vil alle fysiske processer i et bestemt system være kendetegnet ved diskontinuerte forandringer af visse fysiske størrelser.
Alle fysiske størrelser, såsom hastighed, acceleration, kraft, arbejde, energi osv., defineres som sædvanligt, men vi må nu tage hensyn til kvantiseringen af rum, tid og masse. Denne fundamentale »atomisering« medfører, at al bevægelse er diskontinuert, — bevægelser foregår i »spring«. Ligeledes vil alle fysiske processer i et bestemt system være kendetegnet ved diskontinuerte forandringer af visse fysiske størrelser.
Processer i et fysisk system kan beskrives ved ændringer af visse kvantetal hørende til bestemte fysiske størrelser, og for disse kvantetal gælder visse bevarelseslove.
Alle fysiske størrelser kan udtrykkes ved de kosmiske fundamentalstørrelser: rumkvantet, tidskvantet og den totale stof-/energimasse af universet!
De kvantekosmologiske grundligninger. Evolutionskvantetallet
I min holistiske kvantekosmologi med aftagende gravitation, der kan studeres andetsteds, gives en sammenhæng mellem universets aktuelle udstrækning, dets aktuelle alder og elementarlængden og elementartiden. Der angives ligeledes en sammenhæng mellem universets totale stof-/energimasse og den til enhver tid eksisterende elementarmasse. Den koblingsstørrelse, der forbinder universets udstrækning, alder og masse med elementarstørrelserne, kalder jeg for det kosmiske evolutionskvantetal. Dette kosmiske evolutionskvantetal »tikker« op igennem de naturlige tals række. Universet blev »født«, da det kosmiske evolutionskvantetal antog tallet 1.
Det kosmiske evolutionskvantetal bestemmer til enhver tid styrkeforholdet mellem de elektrostatiske og gravitostatiske kræfter mellem en elektron og en positron; – i universets embryonale fase var kræfterne lige store.
De kvantekosmologiske grundligninger kan skrives på følgende måde:
(6) 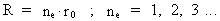 (7)
(7)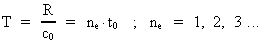 (8)
(8)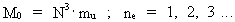 I ligningerne er R universets aktuelle udstrækning, T den hertil hørende
alder, M0 universets totale stof-/energimasse og mu den til
R (eller T) hørende elementarmasse, dvs. massen af én uniton. Det bemærkes,
at de to sidste
ligninger kan udledes fra ligning (6)!
I ligningerne er R universets aktuelle udstrækning, T den hertil hørende
alder, M0 universets totale stof-/energimasse og mu den til
R (eller T) hørende elementarmasse, dvs. massen af én uniton. Det bemærkes,
at de to sidste
ligninger kan udledes fra ligning (6)!
ne er det kosmiske evolutionskvantetal, der også »styrer«
forholdet mellem elektrostatiske og gravitostatiske kræfter efter
sammenhængen:
(9) 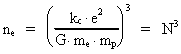 hvor kc er Coulombkonstanten, e det elektriske elementarkvantum,
me elektronens gravitationelle masse, mp positronens
gravitationelle masse og G den aktuelle værdi af gravitations-»konstanten«,
der varierer, efterhånden som det kosmiske evolutionskvantetal »tikker« op igennem de naturlige tal. Idet mp = me gælder, at mp · me = mp² = me². Af ligning (6) ses det, at G aftager efterhånden som universet kvantiseres op i størrelse. Der gælder:
hvor kc er Coulombkonstanten, e det elektriske elementarkvantum,
me elektronens gravitationelle masse, mp positronens
gravitationelle masse og G den aktuelle værdi af gravitations-»konstanten«,
der varierer, efterhånden som det kosmiske evolutionskvantetal »tikker« op igennem de naturlige tal. Idet mp = me gælder, at mp · me = mp² = me². Af ligning (6) ses det, at G aftager efterhånden som universet kvantiseres op i størrelse. Der gælder:
(10) 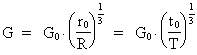 idet universets begyndelsesgravitations-»konstant« G0 er givet ved:
idet universets begyndelsesgravitations-»konstant« G0 er givet ved:
(11) 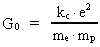 Sammenhængen mellem G0 og G kan således også skrives som:
Sammenhængen mellem G0 og G kan således også skrives som:
(12) 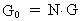
Spaton, tempon og masson — Universets absolutte
fysiske grundenheder
Eksistensen af de fysiske elementarstørrelser, elementarlængden, elementartiden og elementarmassen, betegnet med henholdsvis r0, t0 og m0, viser også den eksisterende mulighed for definitionen af nogle absolutte og fundamentale enheder forde fysiske grundstørrelser, afstand, tidsinterval og masse.
Lad os vedtage følgende:
- Elementarlængden definerer afstandsenheden: 1 spaton, forkortet 1 [sp]
Af lat. spatium: rum
- Elementartiden definerer tidsenheden: 1 tempon, forkortet 1 [te]
Af lat. tempus, -oris: tid
- Elementarmassen definerer masseenheden: 1 masson, forkortet 1 [ma]
Af lat. massa: klump
De kosmologiske enheder 1 spaton og 1 tempon er absolutte og invariante, dvs. de er uafhængige af universets evolution, og de er ligeledes uafhængige af levende væsener og specifikke lokalsystemer. Da de således er uafhængige af vor eksistens, kan de heller ikke afhænge af, hvordan vi som iagttagere evt. bevæger os i forhold til hinanden. Da forholdet mellem r0 og t0 så at sige definerer lysets hastighed c0, ses denne at være ens for alle iagttagere.
Den kosmologiske masseenhed 1 masson er derimod en variabel enhed, idet det antages, at produktet af elementarmassen og det kosmiske evolutionskvantetal er lig en konstant, nemlig universets totale stof-/energimasse. Elementarmassen aftager, efterhånden som universet udvikler sig.
Fysiske størrelser og deres evolutionsligninger i kosmologiske enheder
I det følgende vil vi betragte nogle fysiske størrelser og deres talværdier angivet i kosmologiske enheder.
Da lyskonstanten c0 er givet ved forholdet mellem elementarlængden r0 og elementartiden t0 gælder, at dens talværdi angivet i kosmologiske enheder altid er lig med 1, dvs. der gælder:
(13) 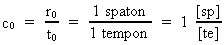 Angivet i kosmologiske enheder gælder der for universets aktuelle udstrækning R, dets alder T og dets masse M0:
Angivet i kosmologiske enheder gælder der for universets aktuelle udstrækning R, dets alder T og dets masse M0:
(14)  (15)
(15)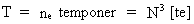 (16)
(16)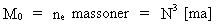 Vi ser det yderst interessante, at de karakteristiske universstørrelser R, T og M0 følges ad med den samme talværdi, nemlig talværdien af det kosmiske evolutionskvantetal. Da universet blev »født«, havde de alle talværdien 1!!
Vi ser det yderst interessante, at de karakteristiske universstørrelser R, T og M0 følges ad med den samme talværdi, nemlig talværdien af det kosmiske evolutionskvantetal. Da universet blev »født«, havde de alle talværdien 1!!
Planck-størrelsen og dens evolutionsligning i kosmologiske enheder
I kosmologiske enheder er Plancks »konstant« en varierende størrelse.
Af ligning (1) får vi:
(17) 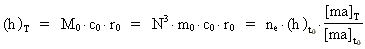 idet vi også har gjort brug af ligningerne (8) og (9).
[ma]T angiver den kosmologiske masseenhed til »tiden«
T, og [ma]t0 er den kosmologiske masseenhed til
»tiden«
1 · t0. Ligning (17) er således en
evolutionsligning for Planck-størrelsen. I øvrigt er
(h)t0 = 1, dvs. Planck-størrelsen
havde talværdien 1, da universet blev
»født«!
idet vi også har gjort brug af ligningerne (8) og (9).
[ma]T angiver den kosmologiske masseenhed til »tiden«
T, og [ma]t0 er den kosmologiske masseenhed til
»tiden«
1 · t0. Ligning (17) er således en
evolutionsligning for Planck-størrelsen. I øvrigt er
(h)t0 = 1, dvs. Planck-størrelsen
havde talværdien 1, da universet blev
»født«!
(h)T er altså en voksende diskret funktion, der øges i takt med universets kvanteekspansion.
Elektronens gravitationelle masse og dens evolutionsligning
Lad os antage, at elektronens gravitationelle masse kan beregnes som en brøkdel af universets totale stof-/energimasse M0. Dvs. der gælder:
(18) 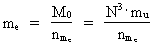 hvor elektronens kosmiske massekvantetal nme antages
konstant i alle enhedssystemer. Til de to »tider« T og
1·t0 gælder da for elektronens masseforhold:
hvor elektronens kosmiske massekvantetal nme antages
konstant i alle enhedssystemer. Til de to »tider« T og
1·t0 gælder da for elektronens masseforhold:
(19) 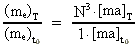 I ligning (19) angiver [ma]T den kosmologiske masseenhed til
»tiden« T, og [ma]t0 den kosmologiske
masseenhed til »tiden«
1·t0.
Disse masseenheder er som nævnt tidligere forskellige.
I ligning (19) angiver [ma]T den kosmologiske masseenhed til
»tiden« T, og [ma]t0 den kosmologiske
masseenhed til »tiden«
1·t0.
Disse masseenheder er som nævnt tidligere forskellige.
Der gælder altså følgende evolutionsrelation
for elektronens masse:
(20) 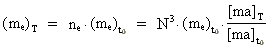
Det elektriske elementarkvantum og dets evolutionsligning
Vi vil nu studere, hvordan evolutionen af det elektriske elementarkvantum foregår.
Til det formål vil vi først omdefinere det elektriske elementarkvantum
e således, at det kan angives udelukkende ved de »mekaniske« grundenheder
for afstand, tidsinterval og masse. Vi inddrager Coulomb-konstanten kc
og definerer en elektromekanisk ladning qe ved:
(21) 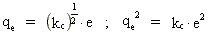 SI-enheden for denne elektromekaniske ladning er: (m/s)·(kg·m)1/2,
altså en enhed med en brøkeksponent.
SI-enheden for denne elektromekaniske ladning er: (m/s)·(kg·m)1/2,
altså en enhed med en brøkeksponent.
Til de to »tider« T og 1·t0 (dvs. da universet blev født)
gælder der følgende:
(22) 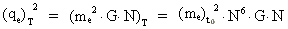 (23)
(23)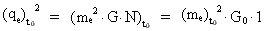 hvor G0 er G's størrelse, da universet blev født,
og hvor et-tallet markerer, at N er lig med 1 til samme »tid«.
hvor G0 er G's størrelse, da universet blev født,
og hvor et-tallet markerer, at N er lig med 1 til samme »tid«.
For den elektromekaniske ladning (qe)T får vi
således følgende evolutionsligning:
(24) 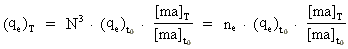 Vi ser, at det igen er det kosmiske evolutionskvantetal, der bestemmer udviklingen.
Vi ser, at det igen er det kosmiske evolutionskvantetal, der bestemmer udviklingen.
Finstruktur-»konstanten« og dens kosmologiske udviklingsligning
Med de foregående resultater kan det let vises, at den såkaldte finstruktur- »konstant«
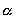 har følgende kosmologiske
evolutionsligning, angivet i kosmologiske enheder: har følgende kosmologiske
evolutionsligning, angivet i kosmologiske enheder:
(25) 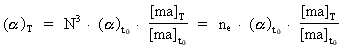 altså samme matematiske formeludtryk som gælder for de andre fysiske størrelser, der er karakteristisk beskrivende for fænomenerne i vort univers.
altså samme matematiske formeludtryk som gælder for de andre fysiske størrelser, der er karakteristisk beskrivende for fænomenerne i vort univers.
Teoretisk påvisning af gravitationens universelle aftagen
Et fundamentalt fysikteoretisk spørgsmål er følgende: Varierer de
fysiske størrelser, som man a priori antager for at være naturkonstanter?
Varierer eksempelvis Plancks konstant, elektronens masse, det elektriske elementarkvantum,
lysets hastighed eller Newtons gravitationskonstant, efterhånden som universet
udvikler sig? Eller er de konstante i rum og tid?
I det foregående har jeg vist, at i de kosmologiske enheder, hvor den kosmologiske
masseenhed varierer med universets desintegration i mindre og mindre massekvanter, i
dette enhedssystem varierer nogle af de fysiske koblingsstørrelser. Variationen af
Newtons gravitations-»konstant« vil fremgå af de følgende
overvejelser, hvor det vises, at variationen af denne er anderledes end for de andre
fysiske størrelser.
Lad os definere en gravitomekanisk ladning mg, der indeholder Newtons
gravitations-"konstant" G og elektronens masse me således at:
(26) 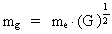 Det kan vises, at der for mg gælder følgende evolutionsligning
angivet i kosmologiske enheder:
Det kan vises, at der for mg gælder følgende evolutionsligning
angivet i kosmologiske enheder:
(27) 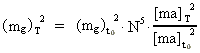 Vi ser, at udviklingsfaktoren i ligning (27) er N5, altså forskellig
fra udviklingsfaktorerne for de andre fysiske størrelser, jeg har betragtet!
Vi ser, at udviklingsfaktoren i ligning (27) er N5, altså forskellig
fra udviklingsfaktorerne for de andre fysiske størrelser, jeg har betragtet!
I kosmologiske enheder vokser denne definerede gravitomekaniske ladning, men lad os nu
transformere til andre, men faste, fysikenheder. Dette kan gøres ved
hjælp af følgende sammenhæng mellem N og de kosmologiske masseenheder
til »tiderne« T og 1·t0:
(28) 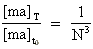 Ved benyttelseaf (28) i ligning (27) får vi:
Ved benyttelseaf (28) i ligning (27) får vi:
(29) 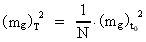 Denne ligning gælder i et vilkårligt enhedssystem med faste invariante
grundenheder.
Denne ligning gælder i et vilkårligt enhedssystem med faste invariante
grundenheder.
Af ligning (29) ser vi det interessante, at den omdefinerede gravitationelle
masse2 af elektronen mg2 aftager omvendt
proportionalt med N. Ved benyttelse af ligningerne (6) og (9) kan vi udtrykke variationen
ved universets aktuelle udstrækning R. Vi får:
(30) 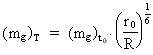 Denne ligning kunne vi også få ud fra ligning (10). Omvendt kan vi nu fra
ligning (30) og ligning (26) få ligning (10), dvs.:
Denne ligning kunne vi også få ud fra ligning (10). Omvendt kan vi nu fra
ligning (30) og ligning (26) få ligning (10), dvs.:
(31) 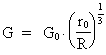 I ligning (31) er G gravitations-»konstanten« til »tiden« T og
G0 dennes størrelse, da universet blev »født«.
I ligning (31) er G gravitations-»konstanten« til »tiden« T og
G0 dennes størrelse, da universet blev »født«.
Hvis vi transformerer ligningerne (17), (20), (24) og (25) til et enhedssystem med
faste grundenheder som f.eks. det almindeligvis benyttede SI-enhedssystem ved brug af
udtrykket i ligning (28), får vi følgende:
(32) 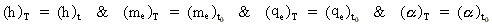 altså at disse størrelser ikke varierer sammen med
universets udvikling. Derimod er det vist, at Newtons
gravitations-»konstant« aftager, efterhånden som
universet i »kvantespring« ekspanderer.
altså at disse størrelser ikke varierer sammen med
universets udvikling. Derimod er det vist, at Newtons
gravitations-»konstant« aftager, efterhånden som
universet i »kvantespring« ekspanderer.
Hvis vi forkorter tredje potens af forholdet
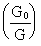 med det store græske
gamma, dvs.: med det store græske
gamma, dvs.:
(33) 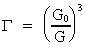 da kan vi få samme udviklingsformel som for de andre fysiske størrelser, nemlig:
da kan vi få samme udviklingsformel som for de andre fysiske størrelser, nemlig:
(34) 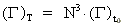 Det skal dog kraftigt understreges, at udviklingsligningen i (34) gælderi alle enhedssystemer, idet den ikke afhænger af forholdet mellem de kosmologiske masseenheder, hvilket er tilfældet for de udviklingsligninger, jeg har ogstillet for de andre fysiske størrelser.
Det skal dog kraftigt understreges, at udviklingsligningen i (34) gælderi alle enhedssystemer, idet den ikke afhænger af forholdet mellem de kosmologiske masseenheder, hvilket er tilfældet for de udviklingsligninger, jeg har ogstillet for de andre fysiske størrelser.
Universets kvanteholistiske formel og dets udvikling gennem naturlige tal
De foregående analyser kan nu samles til en universel helhed, idet jeg har vist, at
der i de kosmologiske enheder gælder følgende sammenhæng mellem
de fysiske størrelser, som vi mennesker har defineret for at kunne beskrive det
univers, vi selv er udsprunget fra:
(35) 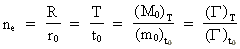 (36)
(36)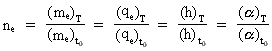 I disse ligninger er ne det kosmiske evolutionskvantetal, der kun
kan antage naturlige tal! Universet udvikler sig i kvantespring, idet
ne »tikker« op igennem de naturlige tal. Universet blev
»født«, da ne antog talværdien 1. Ligningerne (35) og (36)
er universets evolutionsligninger. De eneste fysiske størrelser, som er
universalkonstanter, er: elementarlængden, elementartiden og lyskonstanten. Disse
har alle talværdien 1 i de kosmologiske enheder.
I disse ligninger er ne det kosmiske evolutionskvantetal, der kun
kan antage naturlige tal! Universet udvikler sig i kvantespring, idet
ne »tikker« op igennem de naturlige tal. Universet blev
»født«, da ne antog talværdien 1. Ligningerne (35) og (36)
er universets evolutionsligninger. De eneste fysiske størrelser, som er
universalkonstanter, er: elementarlængden, elementartiden og lyskonstanten. Disse
har alle talværdien 1 i de kosmologiske enheder.
Ligningerne (35) og (36) kan vi formulere i én universel formel: Universets
kvanteholistiske formel:
(37) 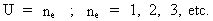 hvor U enten er
hvor U enten er 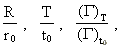 osv. osv.
Hermed er mikrokosmos forenet med makrokosmos, det mindste med det
største!
Maximalværdierne af universets alder og
udstrækning og dets spring mod intetheden
Et interessant spørgsmål er: Har universet en endelig maximal
»leve«-alder, og i bekræftende fald, hvad er denne maximale
alder? Inden for min holistiske kvantekosmologi gives der mulighed for et
talmæssigt svar. Ifølge min kvantekosmologi opdeles universets
stof og energi i mindre og mindre stof-/energi-kvanter, svarende til en mindre
og mindre elementarmasse. Samtidig med denne »nedbrydning« af stof
og energi aftager gravitationen, og universet forøges i geometrisk
størrelse, således at stof og energi kan fordeles i
overensstemmelse med entropiloven.
Muligheden for at beregne universets maximale »leve«-alder ligger
gemt i gravitationens stadige aftagen. Hvis jeg regner i de kosmologiske
enheder, jeg har indført, viser det sig, at gravitations-»konstanten«
startede med en uhyre stor talværdi, da universet blev »født«
for i dag at være nået ned på en betragtelig lavere
talværdi, dog større end 1.
Da universet blev »født«, havde gravitations-»konstanten«
G0 talværdien:
(38) 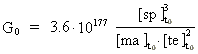
Gravitations-»konstanten« i dag – i vor epoke – kan
beregnes til:
(39) 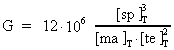
hvilket viser, at gravitations-»konstanten« startede med en uhyre
stor talværdi, da universet blev født for i dag at være
aftaget betragteligt. Det må formodes, at gravitations-»konstanten«
vil aftage ned til talværdien 1 og ikke videre til nul
eller negative tal, da dette ville give ikke-acceptable fysiske tilstande,
eksempelvis føre til afstande mindre end elementarlængden.
Af (38) og (39) fås:
(40) 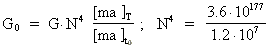
Hvis vi sætter G = 1 i ligning (40), får vi den maximale
talværdi af N, dvs.:
(41) 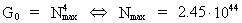
Indsættes denne maximalværdi i den kosmologiske grundligning
for universets alder, dvs. ligningen:
(42) 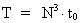
fås:
(43) 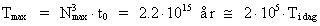
Ved benyttelse af ligning (7) kan universets maximale udstrækning
beregnes:
(44) 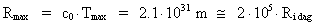
Af den kvantekosmologiske
ligning (8) kan vi beregne mindsteværdien
af den kvantemasse, som universet »lukker og slukker« med.
Om universet derefter vil »springe« mod intetheden, eller om det
kosmiske evolutionskvantetal vil »tikke« baglæns, ja det
må fremtiden vise!
Næste artikel
Hovedsiden
|