Louis Nielsen
Holistisk kvantekosmologi
med
aftagende gravitation
Ny teori om universet
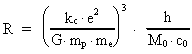
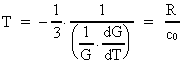
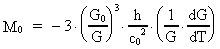
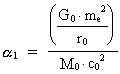
Conditio embryonis omnia determinat
Afhandling
© Copyright 1996 Louis Nielsen
Kvantekosmologi med aftagende gravitation
Kobling af mikro- og makrokosmos
af lektor, cand. scient. Louis Nielsen, Herlufsholm
1. Indledning
I denne afhandling vil jeg fremlægge en teori, der giver en sammenkobling
af mikrokosmos med makrokosmos.
Jeg indfører en elementarlængde og en elementartid.
Min opdagelse af en sammenhæng mellem elementarlængden, universets
nuværende udstrækning, gravitation og elektromagnetisme
fører til den konsekvens, at gravitationen i universet til stadighed
aftager. En formel, der viser hvordan Newtons gravitations-
»konstant« aftager, udledes. Formler, der giver en sammenhæng
mellem universets samlede stof-/energimasse, dets alder og udstrækning
og den relative tidsvariation af gravitations-»konstanten«, udledes
også.
Gravitationens aftagen giver en logisk forståelse af universets
ekspansion og dets struktur med galakser, stjerner og planeter. Som en
naturlig konsekvens af de udledte formler vil jeg postulere følgende:
Hele universet har været samlet inden for et geometrisk område,
der havde en udstrækning lig med elementarlængden. Denne
»fostertilstand« af universet vil jeg kalde for den kosmiske
embryoton. Den her opstillede teori opererer ikke med en
singularitetstilstand! Universet blev »født« inden for det
første kvantetidsinterval! »Samtidig« med universets
»fødsel« opstod de første naturlove - i
»kvantespring«. Den første supernaturlov var entropiloven
(forandringsloven). Denne lov »kræver«, at et system forandrer
sig fra en mindre sandsynlig tilstand til en mere sandsynlig
tilstand. Eller med andre ord: Universet skal udvikle sig fra mere kompakte
tilstande til opdelte og mindre tætte tilstande. Gravitationsloven
»fødtes« med en styrke, der var omkring 1042 gange
større end i dag. Med en stadig aftagende gravitation vil tyngdeloven
kunne opfylde entropilovens »krav«!
Teoriens formler fører til en meget fundamental, yderst lille
massestørrelse. Formlerne viser, at denne
masse aftager, efterhånden som universrummet kvantiseres opad,
og gravitationen aftager! Denne masse må betragtes som det
nuværende univers' mindste kvantum af masse – elementarmassen!
Denne elementarmasse vil jeg give navnet en uniton.
Universet
ender med at desintegrere ned til struktur- og virkningsløse kvanter i
overensstemmelse med entropiloven. I den her fremlagte teori vises det, at
elektrisk ladning er fundamentalt knyttet til gravitationen i det embryonale
univers, ja rent faktisk påvises det, at elektromagnetiske
fænomener er af gravitationel natur. De gravitationelle fænomener
kan beskrives ved en 2-vektorfeltteori, hvor de to gravitationsfelter adlyder
ligninger, der er analoge med de maxwellske ligninger.
Et interessant resultat af den her fremlagte teori er en kosmologisk begrundelse
af atomfysikkens »finstrukturkonstant«. Dennes
talværdi har man ikke tidligere haft nogen fundamental teoretisk
begrundelse for. Her vises det nu, at også denne er bestemt af
tilstanden i det embryonale univers. Universets fostertilstand viser sig
således at være altafgørende for, hvordan og hvorledes
universet udvikler sig! Conditio embryonis omnia determinat! -
Fostertilstanden bestemmer alt!
De fleste fysikere og astronomer har i mange år været klar over,
at Einsteins generelle relativitetsteori (der også er en
gravitationsteori) ikke lader sig forene med kvantefysikken og de andre
teorier for partiklers vekselvirkninger. Som mange har udtrykt det, er
fysikken og astronomien »kørt op i en krog«.
Hvis man vil videre i udforskningen af naturens allerinderste hemmeligheder,
og ønsker at opdage den holistiske teori for mikrokosmos og
makrokosmos, ja, da tyder meget på, at man må forkaste Einsteins
generelle relativitetsteori!
Einsteins generelle relativitetsteori er en matematisk smuk, men kompliceret
teori, der søger at geometrisere universet.
Med fascination, vanetænkning og autoritet er den blevet doceret fra den
ene fysikergeneration til den næste. Man kan og vil ikke slippe den.
De reelle fysiske konsekvenser, der kan udledes af den, er meget få. De
effekter, der skulle bekræfte teorien, er meget få. Det drejer sig
om: 1) Merkurperihelanomalien, 2) Gravitationel fotonafbøjning,
3) Gravitationel bølgelængdeforskydning og
4) Gravitationsbølger. Hertil kommer så nogle matematiske
løsningsmodeller, der fortolkes som »sorte huller« eller
andre supertætte objekter.
De fire omtalte effekter kan forklares på en meget simplere måde,
f.eks. ved den her fremlagte gravitationsteori. De nævnte muligheder for
stofsystemers struktur kan også forstås ud fra den her fremlagte
teori, der påviser, at gravitationen har været omkring 1042 gange
større ved universets fødsel! I den accepterede astrofysik
formodes det, at de supertætte objekter er en sluttilstand af meget
tunge stjerner. I den her forelagte afhandling påvises den formodning,
at de supertætte objekter er fødselstilstande for kommende
stjerner! Universet forløber fra mere strukturerede tilstande til
mindre strukturerede, i overensstemmelse med entropiloven.
Hvis vi kræver, at naturens love skal opfylde »simpelhedens
princip«, vil dette degradere Einsteins generelle relativitetsteori.
Man kan sammenligne med den ptolemæiske geometriske model for
planeternes bevægelse. Den blev mere og mere kompliceret. Først
da man forlod den og gik over til Kopernikus', Keplers og endeligt Newtons
teorier, blev beskrivelsen meget simplere!
En »fyrværkerimodel« for hele universet opstilles, hvor
protogalakser og protostjerner er dannet ved ekspansionsprocesser
forårsaget af en meget hurtigt aftagende gravitation i det tidligeste
univers.
En ny teori for energiproduktion og grundstofdannelse i stjernerne opstilles.
Teorien er baseret på eksistensen af superkerner, dvs. nukleonsystemer
med uhyre høje nukleontal, der henfalder under dannelse af alle de
kendte grundstoffer og med energiproduktion til følge.
En ny teori for planetdannelse gives. Teorien giver en forståelse for
planeternes grundstofsammensætning og indbyrdes størrelse.
Overvejelser om naturlovenes evolution fremlægges også.
2. Elementarlængden og elementartiden. Rum-tidskvantisering
Man kan spørge: Eksisterer der i vort univers en fysisk mindste
rumlig længde r0 og et fysisk mindste tidsinterval
t0?
Ud fra overvejelser af Heisenbergs ubestemthedsrelationer vil jeg svare ja til
ovenstående spørgsmål og postulere, at r0 og
t0 er givet ved:
(2.1) 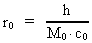
(2.2) 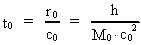
hvor h er Plancks konstant, c0 er lyshastigheden i vacuum, og
M0 er universets totale stof-/energimasse. M0, h og
c0 antages alle at være konstante i rum og tid. Med de kendte
talværdier af c0 og h og en beregnet talværdi
M0 = 1,6 · 1060 kg (se senere!) fås:
(2.3)
Enhver endelig fysisk længde 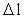 er
bestemt ved et
naturligt tal er
bestemt ved et
naturligt tal 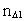 , rumkvantetallet, multipliceret med
r0. Et endeligt tidsinterval er kvantiseret ved et tidskvantetal , rumkvantetallet, multipliceret med
r0. Et endeligt tidsinterval er kvantiseret ved et tidskvantetal
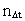 multipliceret med t0. Der gælder
således: multipliceret med t0. Der gælder
således:
(2.4) 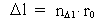 &
&
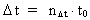
I øvrigt er tidsstørrelsen en af os mennesker indført
størrelse, således at vi på en praktisk måde
kan beskrive og
måle en forandring i et fysisk system. Uden tilstandsforandring i
et fysisk system haves ingen mulighed for at definere en
tidsstørrelse!
Elementarlængden r0 definerer en absolut
kosmologisk længdeenhed, som jeg vil kalde 1 spaton.
Elementartiden t0 definerer en
absolut kosmologisk tidsenhed, som jeg vil kalde 1 tempon.
Disse elementarstørrelser er absolutte i den forstand, at de er
invariante over for en vilkårlig koordinattransformation. r0
divideret med t0 er lig med lyshastigheden c0, der
således meget forståeligt er Lorentz-invariant! Altså
bestemmes til samme talværdi af alle iagttagere!
Elementarlængden r0 og elementartiden t0 skal ikke
opfattes som matematisk eksakte tal, men derimod som
»udtværede« fysiske tal med intervallængderne r0
og t0. De angiver de i princippet fysisk mindste usikkerheder, hvormed
man kan måle afstande og tidsintervaller. Heisenbergs
ubestemthedsrelationer er således en konsekvens af de mere fundamentale
relationer i (2.1) og (2.2)!
3. Universets udstrækning og alder. Gravitationens aftagen
Lad os betragte universets udstrækning R = c0 · T og dets
nuværende alder T. Ifølge (2.4) gælder der:
(3.1) 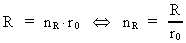
(3.2) 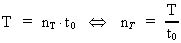
Indsættes i (3.1) og (3.2) de formodede talværdier R og
T, fås:
(3.3) 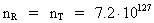
De kosmiske kvantetal nR og nT kan
yderst interessant skrives som:
(3.4) 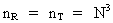
hvor
(3.5)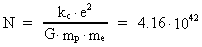
N angiver det nuværende forhold mellem den elektrostatiske og
gravitostatiske tiltrækningskraft mellem en positron og en elektron,
eller blot mellem to elektroner.
G er Newtons gravitations-»konstant« i vor epoke, i dag. Se
senere. kc Coulombkonstanten, e elementarladningen,
me
elektronens gravitationelle masse, og mp positronens
gravitationelle masse.
Ligningerne (3.1) og (3.2) kan nu skrives:
(3.6) 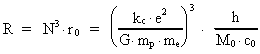
(3.7) 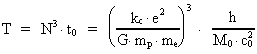
Idet vi må formode, at relationerne (3.6) og (3.7) ikke kun gælder
i vor epoke, men derimod er generelt gyldige for universet i alle dets
tilstande, måske med undtagelse af dets sluttilstand, ser vi
følgende: Efterhånden som universrummet kvantiseres
større og større, dvs. når de kosmiske kvantetal
»tikker« opad, da må en eller flere af størrelserne
G, kc, e, mp, me, h, c0,
M0 variere med R eller
T.
Hvis det antages, at kc, e, mp, me,
h, c0 og M0 ikke
varierer, så er der kun mulighed for en variation af G. Om dette
er tilfældet, kan kun astronomiske og eksperimentelle observationer
vise!
Variationen af G med R og T fås af (3.6) og (3.7)
som:
(3.8) 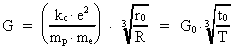
Af (3.8) ser vi, at G aftager, efterhånden som universet
ekspanderer, eller sagt med andre ord: G aftager med den kosmiske tid -
universets aktuelle alder.
Da der ikke eksisterer fysiske tider »før«
t0, kan vi af (3.8) bestemme G's størrelse, da universet
blev »født«, idet der da gjaldt T = t0, dvs.:
(3.9) 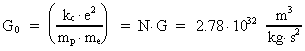
Vi kan således skrive (3.8) som:
(3.10) 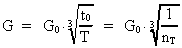
hvilket viser, at gravitationen var omkring 1042 gange større ved
universets »fødsel« end i dag. (3.10) ses at være en
kvantelov.
Af (3.10) får vi for den relative tidsmæssige variation af
G:
(3.11) 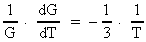
Ligning (3.11) er en af de interessante resultater af den her fremlagte teori,
idet den giver en yderst simpel sammenhæng mellem universets aktuelle
alder T og den relative variation af G. En meget
nøjagtig bestemmelse af denne variation er ønskelig, idet vi
så yderst simpelt kan bestemme universets aktuelle alder af
ligningen:
(3.12) 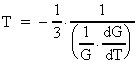
Flere forskere har i tidens løb undersøgt en mulig variation af
G. Alle finder en yderst lille variation og konkluderer, at
gravitationen ikke varierer, idet de fortolker den endelige værdi som et
resultat af måleusikkerhed.
Som ligning (3.11) viser, aftager G i vor epoke uhyre langsomt,
så en meget lille talværdi må forventes!
En af de nyeste analyser er baseret på observationer af
dobbeltpulsarsystemet PSR 1913+16, og man angiver omtrentligt:
(3.13) 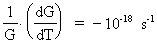
Benyttes talværdien i (3.13) i ligning (3.12), kan vi beregne universets
nuværende alder til:
(3.14) 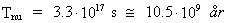
Denne alder for universet passer med de nyeste (1994) aldersanalyser baseret
på målinger foretaget af Hubble-rumteleskopet! Disse
aldersanalyser vurderer, at universet må være mellem 8 milliarder
og 12 milliarder år gammelt.
4. Universets masse bestemt ved variationen af gravitationen
Af ligningerne (3.7) og (3.12) kan vi udlede en formel, der giver en
sammenhæng mellem universets samlede masse M0 og den relative
variation af G. Vi får:
(4.1) 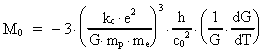
Vi kan også skrive udtrykket i (4.1) på følgende form:
(4.2) 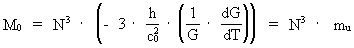
Indsættes talværdier i ligning (4.2), får vi for universets
samlede energi-/stofmasse følgende talværdi:
(4.3) 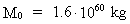
Denne talværdi giver mulighed for utallige både lysende som ikke-
lysende stofsystemer.
Det er denne talværdi, der er benyttet til beregning af
elementarlængdens og elementartidens talværdier.
5. Universets elementarmasse. Unitonen
Man kan spørge: Eksisterer der i vort univers et mindste fysisk kvantum
af masse - en elementarmasse? Og i bekræftende fald: Hvor stor er denne
masse?
Udtrykket i ligning (4.2) giver mulighed for et yderst interessant svar!
Størrelsen afgrænset med den store parentes repræsenterer
nemlig en positiv masse, hvis talværdi til stadighed aftager,
efterhånden som universet udvikler sig! Denne masse må simpelthen
fortolkes som den fysisk mindste masse i det nuværende univers!
Det er universets elementarmasse - kvantemassen! Dette elementarkvantum
vil jeg give navnet en uniton.
Indsættes talværdier, får vi elementarmassens
nuværende størrelse:
(5.1) 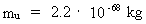
Af ligning (4.2) ser vi, at universet startede med én elementarmasse,
der var lig med universets samlede masse. Universet startede fra en
kvantemasse - den kosmiske embryoton!
Det kan let vises, at mu også kan udtrykkes på
følgende måde:
(5.2) 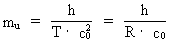
I ligning (5.2) er T universets nuværende alder og R
universets nuværende udstrækning. Udtrykkene i (5.2) er identisk
med massen af en foton med »bølgelængden« R
og svarende til en »frekvens« 1/T.
Af ligning (4.2) ser vi, at mu har noget med gravitation at
gøre, idet dens størrelse er bestemt ved den relative variation
af G.
Denne kendsgerning fører os til følgende: mu
er den nuværende masse af en uniton, de
gravitationelle kræfters årsag og »formidlerpartikel«. I
»fødselstidsrummet« inden for det første
kvantetidsinterval af universet var »unitonens« masse lig med
massen af den kosmiske embryoton. Den aftagende gravitation er
forbundet med universets ekspansion og en aftagende unitonmasse og en dermed
aftagende kosmisk unitontæthed – dvs. antal unitoner pr. rumfangsenhed.
Unitonmassens
nuværende uhyre lille talværdi kan forklare, hvorfor vi har yderst
svært ved at påvise gravitationsbølger.
6. Elektrisk ladning som en gravitationel størrelse
Ligning (3.9) giver en direkte sammenhæng mellem elektrostatik og
gravitostatik! Ligningen giver os mulighed for at udtrykke det elektriske
elementarkvantum e ved gravitationelle størrelser på
følgende måde:
(6.1) 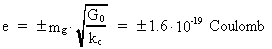
Vi ser meget interessant, at der både er en positiv og en negativ
talværdi, i overensstemmelse med erfarne observationer af elektriske
fænomener! Der observeres både frastødende og
tiltrækkende elektriske kræfter. Vi kan heraf konkludere, at en
elektrons - eller positrons - elektriske ladning er knyttet til dens
gravitationelle masse mg gennem universets initiale
gravitationskonstant G0.
Det er hermed vist, at den elektriske kraft, som man har betragtet som en
selvstændig naturkraft, i realiteten er en »fastfrosset«
gravitationskraft med samme styrke, som da universet blev
»født«!
Da magnetiske kræfter kan vises at være specielle relativistiske
korrektioner til elektriske kræfter, kan vi ultimativt konkludere:
Elektromagnetiske fænomener er i realiteten gravitationsdynamik!
Til dagligdags beskrivelse kan vi naturligvis godt benytte de tillærte
og vante elektromagnetiske begreber.
Alle »elektromagnetiske« fænomener kan beskrives ved de fire
Maxwell-ligninger i kombination med den »elektromagnetiske« Lorentz-
kraft.
Ligningerne kan skrives på følgende måde:
(6.2) 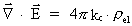
(6.3) 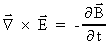
(6.4) 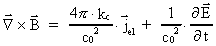
(6.5) 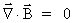
(6.6) 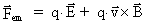
I ligningerne er  den elektriske
feltstyrkevektor, den elektriske
feltstyrkevektor,  den magnetiske
feltstyrkevektor, den magnetiske
feltstyrkevektor,
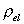 den
elektriske ladningstæthed og den
elektriske ladningstæthed og 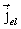 den elektriske ladningsstrømtæthedsvektor.
den elektriske ladningsstrømtæthedsvektor.
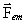 er den
elektromagnetiske kraft på en ladning q, der bevæger sig
med hastigheden er den
elektromagnetiske kraft på en ladning q, der bevæger sig
med hastigheden  . .
 er divergensoperatoren og
er divergensoperatoren og 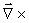 rotationsoperatoren.
rotationsoperatoren.
Man kan i øvrigt vise, at Maxwells ligninger er en konsekvens af
Coulombs elektrostatiske kraftlov og transformationsligningerne for
kræfter som angivet i den specielle relativitetsteori. Da Newtons
gravitostatiske kraftlov er matematisk identisk med Coulombs lov, vil
en tilsvarende matematisk udledning resultere i gyldigheden af nogle
gravitationelle ligninger, der minder om de maxwellske, sådan at
forstå, at man ud over det gravitostatiske felt også skal operere
med et gravitationelt rotationsfelt, der eksisterer omkring graviterende
masser, der bevæger sig. Dette kommer vi tilbage til i et senere
afsnit.
At der i ligning (6.1) indgår Coulombkonstanten kc skyldes den
måde, vi vælger at definere elektrisk ladning på. Ved en
omdefinition er det muligt at fjerne konstanten.
Da det er en eksperimeltel erfaring, at den elektriske ladning af en partikel
er en Lorentz-invariant størrelse, dvs. ikke afhænger af
partiklens hastighed, ser vi af ligning (6.1), at partiklens gravitationelle
masse også er en Lorentz-invariant størrelse.
At gravitationel masse er en Lorentz-invariant størrelse har alvorlige
konsekvenser for Einsteins generelle relativitetsteori fra 1915, idet denne
teori er baseret på identiteten (eller proportionaliteten) mellem
gravitationel masse og inertiel masse. Disse to
massestørrelser en kun identiske for en partikel i hvile, idet den
inertielle masse vokser med hastigheden ifølge den specielle
relativitetsteori.
Hvis de her fremlagte overvejelser er korrekte, må vi konkludere, at
Einsteins generelle relativitetsteori må forkastes som værende en
generel fysisk teori og kun vil kunne benyttes som en alternativteori inden
for et begrænset erfaringsområde!
7. De kvantekosmologiske grundligninger. Evolutionskvantetallet
Lad os resumere de kvantekosmologiske grundligninger, der beskriver universets
kvantemæssige evolution. Ligningerne kan skrives på
følgende form:
(7.1) 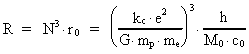
(7.2) 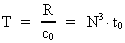
(7.3) 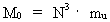
(7.4) 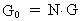
(7.5) 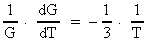
(7.6) 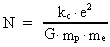
I disse ligninger kan N opfattes som en kosmisk evolutionsoperator.
N³ definerer et kosmisk evolutionskvantetal ne, idet:
(7.7) 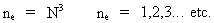
Ligningerne antages at være gyldige fra det første
kvantetidsinterval af universet og til dets »død«,
hvor den samlede energi er delt op i utallige uhyre små
strukturløse kvanter.
Af disse kosmologiske grundligninger kan vi udlede formler, der sætter
os i stand til at beregne universets nuværende udstrækning
Rnu, nuværende alder Tnu og dets samlede stof-
/energimasse M0. For at beregne disse størrelsers
talværdier kræves en nøjagtig bestemmelse af den
nuværende relative variation af G.
Formlerne er:
(7.8) 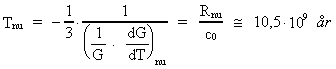
Som det ses, er de kvantekosmologiske ligninger ganske enkle. Dette er ganske
aceptabelt, idet der ikke er noget mærkværdigt i, at desto mere
simpelt et system er, desto mere simple ligninger behøver man til
beskrivelse af systemet. Efterhånden som den kosmiske embryoton brydes
op i mindre og mindre dele, og disse dele også kommer i relativ
bevægelse til hinanden, ja da behøves flere og mere indviklede
ligninger til beskrivelse af systemet. Da evolutionsoperatoren N
så at sige allerede indeholder Newtons gravitostatiske kraftlov og
Coulombs elektrostatiske kraftlov, kan vi ved hjælp af de
specialrelativistiske transformationsligninger udlede de maxwellske ligninger
for elektromagnetisme og de dermed analoge gravitationelle ligninger, idet det
dog bemærkes, at elektromagnetisme også er gravitationsdynamik!
Ligning (7.1) kalder jeg »den universelle formel«, idet de andre
kosmologiske grundligninger enten er indeholdt i denne eller kan udledes fra
denne! Enhedsligningen sammenknytter de »naturkonstanter«, som vi
har fundet i vort metaunivers, dvs. inden for det lokale dagligdags
erfaringsområde. Disse »metanaturkonstanter«, såsom
Plancks konstant, elektronens elektriske ladning, elektronens masse, lysets
hastighed osv. kan i sidste ende udtrykkes ved de kosmiske
fundamentalkonstanter, dvs. universets totale masse, elementarlængden og
elementartiden.
Ligning (7.1) giver en sammenknytning af fysiske størrelser i
mikrokosmos og makrokosmos. Den forener alt i universet!
Nogle kunne indvende, at stærke og svage kernekræfter ikke
indgår i teorien. Hertil vil jeg svare: Disse kræfters virkninger
er også i sidste ende et resultat af gravitationelle virkninger, i vort
metaunivers beskrevet ved elektromagnetiske vekselvirkninger. Protonen og
neutronen kan meget vel bestå af et system af positroner og elektroner.
En stofteori, der er baseret
på disse fundamentale partikler, forklarer også straks, hvor
antistoffet i vort univers befinder sig. Det findes skjult i nukleonerne!
Det bemærkes dog, at alle virkninger og alt stof i sidste ende er et
resultat af unitonernes geometriske fordeling og bevægelsesforhold.
Af udtrykkene i (7.1) og (7.12) kan vi få en sammenhæng mellem
massetæthederne i det embryonale univers og det nuværende
univers.
Vi får:
(7.9) 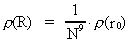
hvor 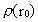 er massetætheden
(massefylden) i det embryonale univers, og er massetætheden
(massefylden) i det embryonale univers, og
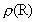 er universets nuværende
massetæthed. er universets nuværende
massetæthed.
Talværdien af 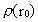 med
M0 givet ved (7.12) er: med
M0 givet ved (7.12) er:
(7.10) 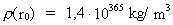
altså et uhyre stort tal, der dog ikke er et matematisk uendeligt tal
som i den etablerede kosmologi baseret på Einsteins generelle
relativitetsteori. I den her fremlagte kosmologiske teori accepteres kun
endelige talværdier. Talværdien af universets nuværende
massetæthed 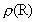 er: er:
(7.11) 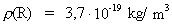
Denne talværdi er meget større end den såkaldte kritiske
massetæthed, som man opererer med i den einsteinbaserede kosmologi. Da
universet endnu er ret »ungt« (10,5 milliarder år), befinder
det sig i en kompaktere tilstand, end hvad man troede før
Hubble-teleskop-æraen. Med en aftagende kosmisk gravitation er en større
massetæthed acceptabel, uden at dette fører til et kosmisk kollaps.
(7.12) 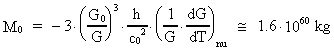
Resultaterne i (7.7) og (7.12), der er en konsekvens af universrummets
kvantisering, skal være med til at bekræfte den her fremlagte
kvantekosmologiske teori.
Nogle kunne måske indvende, at talværdien af universets masse i
ligning (7.12) er rigeligt stor. Forklaringen til dette er, at jeg i ligning
(7.6) har valgt at lade mp være lig med en positrons hvilemasse
og ikke med hvilemassen af en proton. Dette har jeg gjort ud fra den -
filosofiske - betragtning, at jeg opfatter en positron som mere fundamental
end en proton!
Hvis man i udtrykket (7.6) benytter en protons hvilemasse i stedet for en
positrons, vil N blive 1836 gange mindre, og dette vil give en
universmasse, der er (1836)³ gange mindre, nemlig M0 = 2,6 ·
1050 kg. En sådan ændring af N vil dog ikke
ændre på værdierne af R og T.
Talværdien i (7.12) giver mulighed for eksistensen af uhyre
mængder af »mørkt« stof.
Fremtidige observationer og analyser må afgøre realiteterne.
Som det ses, er de kvantekosmologiske ligninger ganske enkle. Dette er ganske
acceptabelt, idet der ikke er noget mærkværdigt i, at desto mere
simpelt et system er, desto mere simple ligninger behøver man til
beskrivelse af systemet. Efterhånden som den kosmiske embryoton brydes
op i mindre og mindre dele, og disse dele også kommer i relativ
bevægelse til hinanden, ja da behøves flere og mere indviklede
ligninger til beskrivelse af systemet. Da evolutionsoperatoren N
så at sige allerede indeholder Newtons gravitostatiske kraftlov og
Coulombs elektrostatiske kraftlov, kan vi ved hjælp af de
specielrelativistiske transformationsligninger udlede de maxwellske ligninger
for elektromagnetisme og de dermed analoge gravitationelle ligninger, idet det
dog bemærkes, at elektromagnetisme også er gravitationsdynamik!
8. Kosmologisk begrundelse af »finstrukturkonstanten«
En størrelse, der spiller en stor rolle i atomfysikken, er den
såkaldte finstrukturkonstant
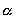 . Den er defineret ved
følgende udtryk: . Den er defineret ved
følgende udtryk:
(8.1) 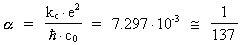
Denne konstant er rent empirisk, idet man ikke har kunnet give en teoretisk
begrundelse for talværdiens størrelse. Jeg kan nu ud fra min
kvantekosmologiske teori give en teoretisk begrundelse af talværdien, der
viser, at denne er bestemt allerede i universets embryonale tilstand. Idet jeg
ikke benytter h 'streg' men h, vil jeg betragte
størrelsen 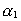 givet ved: givet ved:
(8.2) 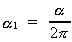
Ved benyttelse af udtrykket i ligning (6.1) omskriver vi
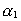 til: til:
(8.3) 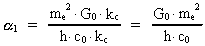
Dette udtryk omskrives, idet der divideres med elementarlængden
r0 både i tæller og nævner. Vi får da
følgende meget interessante udtryk:
(8.4) 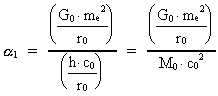
Udtrykket i (8.4) viser, at 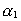 og dermed
»finstrukturkonstanten« er bestemt ved forhold gældende i det
embryonale univers, nemlig følgende: og dermed
»finstrukturkonstanten« er bestemt ved forhold gældende i det
embryonale univers, nemlig følgende: 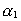 er
bestemt af brøkforholdet mellem den gravitationspotentielle energi af to
elektroner i en elementarlængdes afstand fra hinanden og den totale energi af hele
universet!! er
bestemt af brøkforholdet mellem den gravitationspotentielle energi af to
elektroner i en elementarlængdes afstand fra hinanden og den totale energi af hele
universet!!
Af det foregående ser vi tydeligt, at der eksisterer en fundamental
kobling af mikrokosmos med makrokosmos! G0 er universets initiale
gravitationskonstant givet ved ligning (3.9).
9. En to-vektorfelt gravitationsteori med variable
koblings-»konstanter«
I 1972 foreslog denne artikels forfatter en to-felt gravitationsteori, der i
sin matematiske struktur er identisk med de maxwellske ligninger i
elektrodynamikken. Artiklen er offentliggjort i tidsskriftet GAMMA nr. 9,
februar 1972, der udgives af Niels Bohr Instituttet.
Ud over det gravitostatiske »Newtonfelt«, der er til stede omkring
relativt hvilende graviterende masser, dannes et dynamisk rotationsfelt
omkring graviterende masser, der er i relativ bevægelse.
Dette dynamiske vektorfelt
 tilfredsstiller sammen med det gravitostatiske vektorfelt
tilfredsstiller sammen med det gravitostatiske vektorfelt
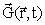 følgende
differentialligninger: følgende
differentialligninger:
(9.1) 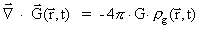
(9.2) 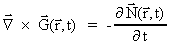
(9.3) 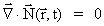
(9.4) 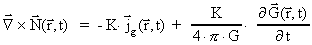
I ligningerne er
 divergensoperatoren, divergensoperatoren,
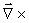 rotationsoperatoren, rotationsoperatoren,
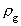 er
den gravitationelle massedensitet og er
den gravitationelle massedensitet og
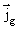 den
gravitationelle massestrømtæthedsvektor. den
gravitationelle massestrømtæthedsvektor.
K er koblings-»konstanten« til det dynamiske
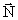 -felt. K kunne kaldes den
gravitationelle permeabilitet. -felt. K kunne kaldes den
gravitationelle permeabilitet.
Sammenhængen mellem K og G er givet ved:
(9.5) 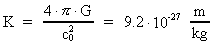
Talværdien gælder i vor epoke, hvor den altså er meget
lille. Dette forklarer, hvorfor man ikke umiddelbart observerer virkningen af
N-feltet.
Kraftloven, der hører til felterne
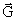 og og
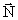 , er givet ved: , er givet ved:
(9.6) 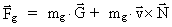
hvor 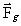 er den kraft, der virker
på en graviterende masse mg, der bevæger sig
med hastigheden er den kraft, der virker
på en graviterende masse mg, der bevæger sig
med hastigheden  i et kombineret i et kombineret
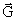 - og - og
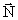 -felt. -felt.
De gravitationelle ligninger forudsiger umiddelbart eksistensen af
gravitationsbølger.
Man kan vise, at Maxwells ligninger er en konsekvens af Coulombs
elektrostatiske kraftlov og transformationsligningerne for kræfter som
angivet i den specielle relativitetsteori. Da Newtons gravitostatiske kraftlov
er matematisk identisk med Coulombs lov, vil en tilsvarende matematisk
udledning resultere i gyldigheden af de gravitationelle ligninger (9.1) til
(9.6).
En analyse af universets udvikling baseret på disse ligninger vil
være af yderst stor interesse, idet det vil give mulighed for en
forståelse af dets struktur, som vi i realiteten observerer det!
Specielt vil galaksestrukturer kunne »forklares«, og ligeledes de
informationer fra objekter i det ydre univers, såsom kvasarer, der jo
giver os informationer om strukturer i det tidligste univers!
Det interessante er nu, at K også er en aftagende
størrelse ligesom G. Ved universets fødsel var K
omkring 1042 gange større end i dag! Talværdien ved universets
fødsel var:
(9.7) 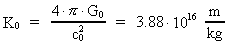
Dette giver mulighed for en helt anden kosmisk struktur end den, der er
baseret alene på ét G-felt! I dag ved man, at universets
galaksestruktur langtfra er homogen. Tværtimod viser det en
uregelmæssig »netstruktur«!
Det ville være ønskeligt med en analyse baseret på den her
foreslåede to-feltsgravitationsteori med variable koblingskonstanter,
specielt en analyse af de dynamiske forhold kort tid efter universets
fødsel til »tidspunktet« t0.
I det allertidligste univers var både G-feltet og det dynamiske
N-felt uhyre store. Da G ændrede sig meget hurtigt, og
massestrømtæthederne var meget store, ser man af ligning (9.4),
at der blev genereret et meget stort N-felt. Som det er bemærket,
følger det umiddelbart af de gravitationelle ligninger, at der kan
genereres gravitationsbølger. Energitætheden i de
gravitationsbølger, der blev genereret umiddelbart efter universets
fødsel, var uhyre stor. Efterhånden som universet ekspanderede,
formindskedes energitætheden. Man må formode, at universet er
fyldt med denne gravitationelle kosmiske baggrundsstråling, helt analogt
til den elektromagnetiske baggrundsstråling. Denne kosmiske
gravitationelle baggrundsstråling bør man søge efter,
når den projekterede LIGO-detektor (Laser Interferometer Gravitational-
wave Observatory) under ledelse af Rochus E. Vogt sættes i drift!
Joseph Weber fra University of Maryland rapporterede i 1969, at han havde
registreret gravitationsbølger fra centret af vor galakse. Der kan
være tale om enorme gravitationelle processer fra resterne af en
galakseembryoton.
En galakseembryoton - galaksefosterpartikel - er en meget koncentreret energi-
»klump«, der blev udsendt af den kosmiske embryoton, endnu mens
gravitationen aftog uhyre hurtigt i det allertidligste univers!
10. Kosmisk fyrværkerimodel. Galakseembryotoner og
stjerneembryotoner
I fortsættelse af betragtningerne i afsnit 9 kan opstilles
følgende fyrværkerimodel for universet: Hele universet
blev dannet ud fra den kosmiske embryoton. I de første kosmiske
kvantetidsrum efter universets begyndelse, hvor gravitationen aftog uhyre hurtigt,
udslyngedes et meget stort antal galakseembryotoner - fosterpartikler
for galakserne.
Under den endnu hurtige aftagen af gravitationen udslyngedes fra hver
galakseembryoton milliarder af stjerneembryotoner. Af disse
stjerneembryotoner dannedes stjernerne i vort univers.
Med hensyn til grundstofdannelsen i vort univers lægger de
foregående betragtninger op til følgende hypotese:
Grundstofferne, specielt dem tungere end jern, er dannet ved desintegration,
naturlig fission og henfald af supertunge kerner med uhyre høje
nukleontal. Grundstofferne er blevet dannet, efterhånden som de fysiske
forhold var til stede i det ekspanderende univers.
Galakseembryotonerne er eksplosionsagtigt sendt ud fra den kosmiske embryoton,
således at de roterer relativt til hinanden, og således at det
totale impulsmoment er nul. Disse roterende galakseembryotoner har -
forårsaget af den endnu hurtige aftagende gravitation - udsendt
stjerneembryotoner. En galakse er under dannelse! Impulsmomentet af
galakseembryotonen fordeles ud til de dannede stjerner, dels som et
baneimpulsmoment, dels som et egenimpulsmoment. De yderste stjerner i den
dannede galakse er kastet ud med den største »slyngkraft«,
hvilket resulterer i en relativt større galaktisk banehastighed end de
sidst udslyngede stjerneembryotoner. Dette galaktiske
bevægelsesmønster er netop observeret i mange galakser.
Hypoteserne om eksistensen af eventuelt »koldt mørkt stof«
behøves således ikke!
Kvasarerne, der befinder sig i milliarder af lysårs afstand fra os, har
også givet forståelsesproblemer, specielt den enorme
energiudstråling fra et relativt lille rumområde. Forklaringen
kunne være, at en kvasar er en galakse under udvikling, og hvor
kvasarcentret er resterne af en galakseembryoton. Da det er objekter i de ydre
dele af universet, ser vi via de elektromagnetiske stråler de fysiske
forhold, som de var i det unge univers, hvor blandt andet gravitationen var
meget større. Resterne af en galakseembryoton svarer sandsynligvis til
det, der i den etablerede kosmologi kaldes »et sort hul«.
Målinger foretaget af Hubble-rumteleskopet i november 1994 viser, at der
i det yderste univers - altså i universets tidligste »barndom«
- eksisterede supertætte objekter og galaksestrukturer. Dette er helt i
modstrid med de accepterede teorier!
Lad os betragte stjernedannelser ud fra en stjerneembryoton. Efterhånden
som gravitationen aftager, desintegrerer stjerneembryotonen for på et
bestemt tidspunkt at blive til uhyre tunge og roterende »klumper« af
neutroner - til nogle i universet roterende neutronkugler! Af disse
neutronkugler er stjernerne dannet! Disse neutronkugler må antages at
være identiske med nogle af de pulsarer, vi i dag har kendskab til. Som
det kan forstås, er pulsarerne - ifølge den her fremlagte teori -
ikke sluttilstande af stjerner, men derimod begyndelsestilstande af nye
stjerner! Universet er endnu relativt ungt, hvilket betyder, at der
ifølge de accepterede teorier for pulsardannelse og »sort
hul«-dannelse ikke har været tid nok!
Lad os betragte stjernedannelser ud fra en stjerneembryoton. Efterhånden
som gravitationen aftager, desintegrerer stjerneembryotonen for på et
bestemt tidspunkt og under bestemte forhold at blive til en »klump«
neutroner - en i universet roterende neutronkugle. Af disse neutronkugler er
stjernerne dannet - hvis ikke alle stjerner, da de ældste. Disse
neutronkugler må antages at være identiske med nogle af de
pulsarer, vi i dag har kendskab til.
Omkring de hurtigt roterende neutronkugler er dannet et stærkt
magnetfelt. Som et resultat af dette stærke magnetfelt (og måske
den kvantemekaniske tunneleffekt) »blæses« klynger af
neutroner og enlige neutroner ud fra neutronkuglens overflade. Idet nogle af
neutronerne omdannes til protoner, elektroner og antineutrinoer, vil der under
de ekstreme forhold blive dannet et utal af superkerner (en bedre
betegnelse ville nok være makrokerner), der er defineret ved at
have uhyre høje nukleontal.
11. Ny fissions-fusions-model for stjernerne med centralkerne af
neutroner
I det følgende beskrives en ny model for solen og andre lignende
stjerner. Lad os, som eksempel, betragte solens opbygning og de processer, der
foregår i den.
Generelt betragtet har solen en lagdelt struktur og funktion. Den centrale del
består af en relativt lille roterende neutronkugle, der alene
består af neutroner. Denne roterende neutronkugle er kilden til solens
primære magnetfelt. Omkring neutronkuglen eksisterer en zone af
superkerner med forskellige, meget høje nukleontal. Disse superkerner
er »fordampet« fra neutronkuglens overflade, hjulpet afsted af det
stærke magnetfelt og evt. af den kvantemekaniske tunneleffekt.
I denne superkernezone forløber henfald af superkerner ved
spontan og induceret fission og ved 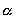 -, -,
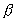 -, -,
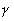 - og - og
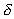 -processer. Disse processer er
energiproducerende, og samtidig dannes de tungere grundstoffer ned til jern,
der er den mest stabile kerne, vi har kendskab til. De neutroner, -processer. Disse processer er
energiproducerende, og samtidig dannes de tungere grundstoffer ned til jern,
der er den mest stabile kerne, vi har kendskab til. De neutroner,
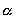 -partikler og lettere grundstofkerner,
der dannes ved superkernernes fission og
efterfølgende henfald, »blæses« af
strålingstrykket og partikeltrykket udad i solen. Neutronerne omdannes
til protoner, elektroner og antineutrinoer, hvorfra der kan dannes
hydrogenatomer. -partikler og lettere grundstofkerner,
der dannes ved superkernernes fission og
efterfølgende henfald, »blæses« af
strålingstrykket og partikeltrykket udad i solen. Neutronerne omdannes
til protoner, elektroner og antineutrinoer, hvorfra der kan dannes
hydrogenatomer. 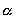 -partikler giver
mulighed for dannelsen af
heliumatomer. I superkernezonen bliver hyppigheden af specielt jern
større og større, efterhånden som desintegrationen af
superkernerne skrider frem. Hydrogen, helium og nogle af de lettere og
tungere grundstoffer »placerer« sig i to zoner omkring og uden for
superkernezonen. I den inderste hydrogen-heliumzone, hvor temperatur og tryk
er høje, foregår der fusionsprocesser under frigørelse af
energi og dannelse af de lettere grundstoffer. Den anden hydrogen-heliumzone
er identisk med de yderste dele af solen og består, som spektralanalyse
viser, af hydrogen, helium og lettere grundstoffer, heri iblandet
»lidt« tungere grundstoffer. -partikler giver
mulighed for dannelsen af
heliumatomer. I superkernezonen bliver hyppigheden af specielt jern
større og større, efterhånden som desintegrationen af
superkernerne skrider frem. Hydrogen, helium og nogle af de lettere og
tungere grundstoffer »placerer« sig i to zoner omkring og uden for
superkernezonen. I den inderste hydrogen-heliumzone, hvor temperatur og tryk
er høje, foregår der fusionsprocesser under frigørelse af
energi og dannelse af de lettere grundstoffer. Den anden hydrogen-heliumzone
er identisk med de yderste dele af solen og består, som spektralanalyse
viser, af hydrogen, helium og lettere grundstoffer, heri iblandet
»lidt« tungere grundstoffer.
Disse superkerner kan under bestemte fysiske forhold desintegrere og henfalde
ved forskellige reaktionstyper. En bestemt superkerne kan henfalde ved bl.a.
successive multifissioner - naturlige som inducerede -
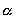 -, -,
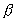 -, -,
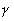 - og - og
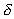 -henfald. Med -henfald. Med
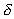 -henfald betegnes under ét alle
andre partikelemissioner end -henfald betegnes under ét alle
andre partikelemissioner end
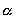 , ,
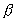 og og
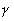 .
Eksempelvis kan der
være tale om emission af carbonkerner, oxygenkerner, siliciumkerner,
svovlkerner etc. Ved desintegrationsprocesserne frigøres der energi,
der viser sig i form af kinetisk energi og strålingsenergi.
Partikeltrykket og strålingstrykket bevirker en »oppustning«
af stofsystemet. En aktiv stjerne er under dannelse. .
Eksempelvis kan der
være tale om emission af carbonkerner, oxygenkerner, siliciumkerner,
svovlkerner etc. Ved desintegrationsprocesserne frigøres der energi,
der viser sig i form af kinetisk energi og strålingsenergi.
Partikeltrykket og strålingstrykket bevirker en »oppustning«
af stofsystemet. En aktiv stjerne er under dannelse.
Med hensyn til den mulige eksistens af superkerner, så er kondensationen
af et mangepartikelsystem allerede teoretisk forudsagt af Einstein og Bose for
omkring 70 år siden, og i 1995 lykkedes det for første gang at
»skabe« et sådant Bose-Einstein-kondensat. Så i det
store univers, hvor alle mulige fysiske tilstande forekommer, er -
næsten - alt muligt!
Stjernemodellen kan resumeres som følger:
- Inderst: Roterende neutronkugle:
- En relativt hurtigt roterende neutronkugle, der er kilde til stjernens
primære magnetfelt. Den er også kilde til de superkerner, der
»blæses« ud fra overfladen.
- Dernæst følger: Superkernezonen - Fissionszonen:
- En zone bestående af superkerner, der desintegrerer og henfalder
under energifrigørelse og samtidig dannelse af de tungere grundstoffer
ned til jern.
- Så følger: Jernzonen:
- En zone med relativt stor hyppighed af jern, og hvor der er
»balance« mellem fissionsprocesser og fusionsprocesser.
- Så følger: H-He-zone 1 - fusionszonen:
- En zone bestående primært af hydrogen og helium, og hvor der
forløber fusionsprocesser under energifrigørelse og dannelse af
de lettere grundstoffer.
- Og yderst haves: H-He-zone 2 - fusionsfri zone:
- En zone bestående af hydrogen, helium og lettere grundstoffer, heri
iblandet tungere grundstoffer.
Den yderste zone kender vi ganske godt gennem studier af spektre. Derimod er
informationer fra de andre zoner for nuværende vanskelige at analysere.
Her er det studier af neutrinoflux, magnetfelter og helioseismologi, der skal
be- eller afkræfte den her opstillede model. Teorien kan måske
også bekræftes således: Den indre roterende neutronkugle med
det stærke magnetfelt vil give anledning til udstråling af
pulsarlignende radiobølger udsendt i en kegle langs med den magnetiske
akse. Denne radiostråling vil dog blive forvrænget på sin
vej ud igennem solens sekundære magnetfelt, dannet af elektrisk ladede
partiklers bevægelse.
Denne radiostråling kan måske påvises af instrumenterne
ombord i satellitten »Ulysses«, der skal bevæge sig
forbi solens poler i 1995.
Hvis den her foreslåede teori for energiproduktion og grundstofdannelse
i solen skal bekræftes, skal man også måle på den
neutrinoflux, der forlader solen. Dette er også gjort, men med det
resultat, at man kun har registreret omkring 1/3 af de neutrinoer, man skulle
registrere ifølge beregninger baseret på en »ren«
fusionsmodel. Dette er en stor »gåde«, så måske er
løsningen den her opstillede model. Da man ikke kender de helt
specifikke reaktioner for superkernernes desintegration, er det endnu ikke
muligt at beregne den emitterede neutrinoflux.
Den her fremlagte teori er mere i overensstemmelse med entropiloven, der
»dikterer«, at et system skal søge imod en tilstand med
større sandsynlighed - større uorden! Fusionsprocesser, der
resulterer i et mere struktureret system, strider faktisk imod entropiloven.
Lokalt og midlertidigt kan entropien dog sænkes og holdes konstant, selv
om den totalt set altid vil stige. Man må formode, at naturen under
bestemte forhold altid »vælger« de simpleste og mest direkte
processer.
Vogtet og dikteret af entropiloven ender hele universet som en
»suppe« af strukturløse partikler.
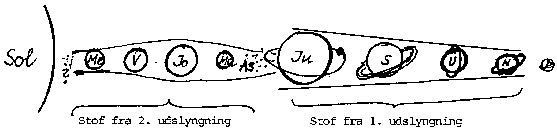
12. Ny teori for dannelsen af planeterne og deres måner
Stoffet, der har dannet planeterne, er udslynget af en allerede aktiv sol,
hvor energiproduktionen og grundstofdannelsen er godt i gang.
Det præplanetariske stof er »rotations«-udslynget ved en
to-trins eksplosivmekanisme. De yderste planeter med mindst massefylde
er dannet først. De inderste planeter med størst massefylde er
dannet sidst. De yderste planeter, Neptun, Uranus, Saturn og Jupiter, er
således de ældste. De inderste planeter, Mars, Jorden, Venus og
Merkur, er de yngste.
Lad os først betragte dannelsen af de ydre planeter. Til et bestemt
tidspunkt er der forekommet en ustabilitet i den aktive sol, således at
en eksplosionsproces er startet. De yderste hydrogen- og helium-holdige
stoflag af solen er blevet slynget ud i rummet, hvor det har lejret sig i en
roterende præplanetarisk stofring. På grund af solens
gravitationelle træk trækkes stoffet mod solen. Dette resulterer i
to effekter: Dels at den oprindelige stofskive er blevet delt op i flere
adskilte ringsystemer, dels at mængden af stof er blevet størst
nærmest solen. I tidens løb er de forskellige stofringe blevet
kondenseret til de forskellige ydre planeter. Den største planet,
Jupiter, tættest ved solen og derefter med aftagende størrelse
udad til Neptun. (Pluto er sandsynligvis en planet, der har
»forvildet« sig ud i de ydre dele af solsystemet). I dag vides det
fra analyser, at de ydre planeter fortrinsvis består af hydrogen og
helium, heri iblandet nogle tungere grundstoffer. Meget bedre viden om
grundstofsammensætningen får vi i løbet af 1996, når
vi modtager data fra Galileo-rumsonden, der i december 1995 er blevet sat ind
i et to-årigt kredsløb omkring Jupiter, efter at en
instrumentkapsel med stor succes har gennemtrængt over 100 km af
Jupiters meget tætte atmosfære.
Efter soleksplosionsprocessen er det udadrettede strålings- og
partikeltryk faldet. Dette bevirker en gravitationel sammentrækning af
de yderste stoflag af solen, der nu har en langt større hyppighed af
tungere grundstoffer, specielt jern.
En efterfølgende (i tid sandsynligvis længe efter den
første) 2. soleksplosion slynger stof ud, der er righoldigt på
tungere grundstoffer, specielt jern. Af dette stof er de indre planeter,
Merkur, Venus, Jorden, Mars og asteroiderne, dannet. Men af dette stof
består også de måner og stofringe, der kredser omkring de
ydre planeter fra Jupiter og udefter. Stoffet er simpelthen blevet indfanget
af planeternes tyngdefelt for derefter at gå i omløb omkring
planeterne. Hermed er således forklaret, hvorfor de måner og det
stof, der kredser omkring de ydre planeter, består af jordlignende
grundstoffer. Dette løser en hidtil stor »gåde«!
Stoffet mellem solen og Jupiter, der roterer omkring solen, udsættes for
to gravitationelle træk. Et, der prøver at trække stoffet
mod solen, og et, der trækker stof ud imod Jupiter. Denne totræks-
effekt bevirker to ting. Dels at stofskiven deles op i 5 stofskiver; dels at
stofskiverne nærmest solen og Jupiter er »fladest«, og den
skive, der befinder sig »midt« mellem solen og Jupiter, er tykkest.
Af denne er Jorden dannet. De mindste planeter, Merkur og Venus og dem, der
indeholder de tungeste grundstoffer, specielt jern, er dannet nærmest
solen. Af stofringene nærmest Jupiter er Mars og asteroiderne dannet.
Stofringen nærmest Jupiter har ikke kunnet kondensere sig til en planet
på grund af Jupiters store tyngdekraft. Noget tilsvarende vil også
gælde for en eventuel stofring mellem solen og Merkur. Mindre og
større stofklumper eksisterer sandsynligvis i banebevægelse inden
for Merkurs bane. På grund af det stærke sollys er de yderst
vanskelige at observere. Eksistensen af disse stofklumper vil kunne give en
forklaring på Merkurperihelanomalien! Einsteins gravitationsteori er
således ikke nødvendig!
At Merkur næsten er en stor jernkugle, der bevæger sig omkring
solen, er således fuldt forståeligt.
Måner og stofringe bestående af
tungere grundstoffer er dannet af
stof fra 2. stofudslyngning!
|
|
|
13. Universets superfundamentale naturkonstanter og
evolutionsparametre
I menneskets søgen efter sandhed stilles spørgsmål som:
Hvem er vi, hvorfra kommer vi, og hvortil går vi? Hvem, hvad og hvordan
styres alle de processer, der foregår i vort univers? Hvad er det hele
for noget?
I fysikken - der mest systematisk og objektivt - søger svaret på
ovenstående spørgsmål, har man opdaget eksistensen af et
sæt fysiske størrelser, der bestemmer koblingen og styrken af de
processer, der forløber i et betragtet system. Disse fysiske
størrelser er de såkaldte naturkonstanter. Eksempler
på sådanne konstanter er: Lysets hastighed i vacuum c0,
Plancks konstant h, Newtons gravitationskonstant G, det
elektriske elementarkvantum e, elektronens masse me, Boltzmanns
konstant k etc.
Spørgsmålene er nu: 1) Er sættet af kendte naturkonstanter
uafhængigt af hinanden, eller afhænger nogle af hinanden? 2) Er
de kendte naturkonstanter de mest fundamentale i vort univers, eller
eksisterer der nogle superfundamentale natur-»konstanter«, hvoraf de
andre kan afledes? Og ikke mindst 3) Er de konstante eller varierer alle
eller nogle af dem, efterhånden som universet udvikler sig?
Jeg mener, at de natur-»konstanter«, som vi i vore teorier i dag
arbejder med, er konstanter på et højere niveau end de mest
fundamentale. De kan afledes af de superfundamentale naturstørrelser.
Hvilke størrelser er så de superfundamentale? Det er: Den totale
felt- og stofmasse af universet, M0, elementarlængden r0
og elementartiden t0!
Til dette sæt af størrelser må lægges en
evolutionsparameter, der er »ansvarlig« for, at universet
overhovedet eksisterer og gennemløber en evolution! Denne
evolutionsparameter er størrelsen N og potenser deraf!
Antallet af partikler i det nuværende univers er af størrelsen
N². Universets absolutte entropi er en funktion af N.
Da universet blev dannet, var entropien lig med nul.
Et af hovedresultaterne i den her fremlagte teori er sammenkoblingen af
mikrokosmos med makrokosmos - det er en holistisk teori! Den determinerende
og mest fundamentale størrelse i vort univers er dets masse M0.
M0 er således bestemmende, sammen med elementarlængden og
elementartiden, for størrelserne af de koblingskonstanter, der
indgår i de fysiske love!
Det kan formodes, at de fysiske love undergår en evolution - ligesom alt
andet - således, at nogle »fødes« med senere mulighed
for mutationer, mens andre »dør« og således, at det er
de »stærkeste« love, der fortrinsvis vil afgøre,
hvordan universets evolution og struktur forløber.
Informationerne om naturlovenes struktur er »nedlagt« allerede i
universets fostertilstand! Conditio embryonis omnia determinat!
Ultimativt uddør alle love!
Louis Nielsen
E-mail: louis44nielsen@gmail.com
Den her fremlagte kosmologiske teori er et resultat af over 25 års
spekulationer over det fysiske univers. Ønsket har hele tiden
været at forene makrokosmos med mikrokosmos. Det filosofiske
arbejdsprincip har været og er stadig: Universets starttilstand
bestemmer alt!
Næste artikel
Hovedsiden
|
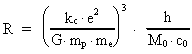
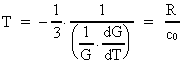
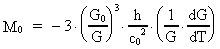
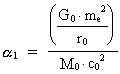
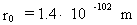
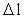 er
bestemt ved et
naturligt tal
er
bestemt ved et
naturligt tal 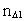 , rumkvantetallet, multipliceret med
r0. Et endeligt tidsinterval er kvantiseret ved et tidskvantetal
, rumkvantetallet, multipliceret med
r0. Et endeligt tidsinterval er kvantiseret ved et tidskvantetal
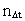 multipliceret med t0. Der gælder
således:
multipliceret med t0. Der gælder
således: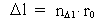 &
&
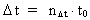
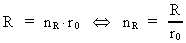
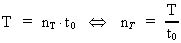
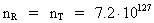
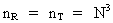
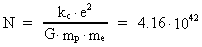
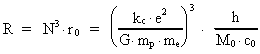
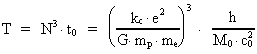
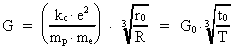
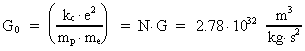
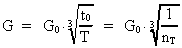
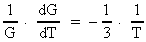
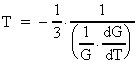
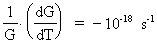
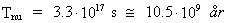
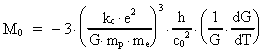
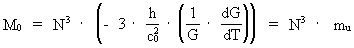
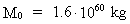
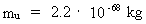
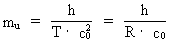
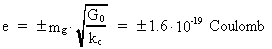
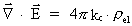
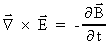
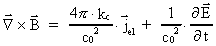
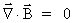
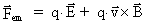
 den elektriske
feltstyrkevektor,
den elektriske
feltstyrkevektor,  den magnetiske
feltstyrkevektor,
den magnetiske
feltstyrkevektor,
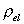 den
elektriske ladningstæthed og
den
elektriske ladningstæthed og 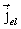 den elektriske ladningsstrømtæthedsvektor.
den elektriske ladningsstrømtæthedsvektor.
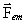 er den
elektromagnetiske kraft på en ladning q, der bevæger sig
med hastigheden
er den
elektromagnetiske kraft på en ladning q, der bevæger sig
med hastigheden  .
.
 er divergensoperatoren og
er divergensoperatoren og 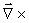 rotationsoperatoren.
rotationsoperatoren.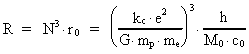
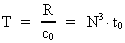
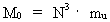
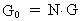
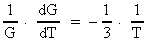
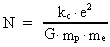
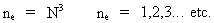
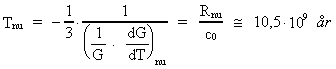
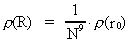
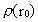 er massetætheden
(massefylden) i det embryonale univers, og
er massetætheden
(massefylden) i det embryonale univers, og
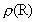 er universets nuværende
massetæthed.
er universets nuværende
massetæthed.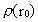 med
M0 givet ved (7.12) er:
med
M0 givet ved (7.12) er: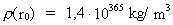
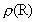 er:
er: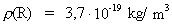
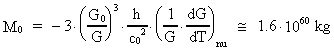
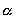 . Den er defineret ved
følgende udtryk:
. Den er defineret ved
følgende udtryk: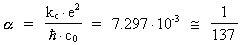
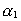 givet ved:
givet ved: 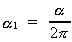
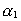 til:
til: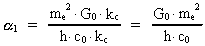
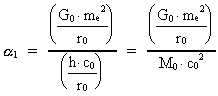
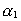 og dermed
»finstrukturkonstanten« er bestemt ved forhold gældende i det
embryonale univers, nemlig følgende:
og dermed
»finstrukturkonstanten« er bestemt ved forhold gældende i det
embryonale univers, nemlig følgende: 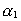 er
bestemt af brøkforholdet mellem den gravitationspotentielle energi af to
elektroner i en elementarlængdes afstand fra hinanden og den totale energi af hele
universet!!
er
bestemt af brøkforholdet mellem den gravitationspotentielle energi af to
elektroner i en elementarlængdes afstand fra hinanden og den totale energi af hele
universet!!
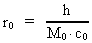
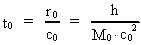
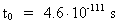
 tilfredsstiller sammen med det gravitostatiske vektorfelt
tilfredsstiller sammen med det gravitostatiske vektorfelt
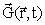 følgende
differentialligninger:
følgende
differentialligninger: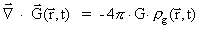
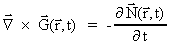
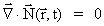
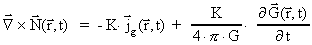
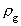 er
den gravitationelle massedensitet og
er
den gravitationelle massedensitet og
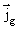 den
gravitationelle massestrømtæthedsvektor.
den
gravitationelle massestrømtæthedsvektor.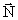 -felt. K kunne kaldes den
gravitationelle permeabilitet.
-felt. K kunne kaldes den
gravitationelle permeabilitet.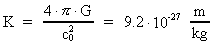
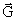 og
og
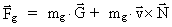
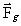 er den kraft, der virker
på en graviterende masse mg, der bevæger sig
med hastigheden
er den kraft, der virker
på en graviterende masse mg, der bevæger sig
med hastigheden 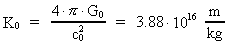
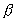 -,
-,
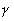 - og
- og
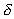 -processer. Disse processer er
energiproducerende, og samtidig dannes de tungere grundstoffer ned til jern,
der er den mest stabile kerne, vi har kendskab til. De neutroner,
-processer. Disse processer er
energiproducerende, og samtidig dannes de tungere grundstoffer ned til jern,
der er den mest stabile kerne, vi har kendskab til. De neutroner,