|
New Cosmological Model of the Electron The Electron – a Uniton Dynamical Subsystem in the Cosmic
Uniton Field
By Louis Nielsen, Senior Physics Master, Herlufsholm Introduction: What is an electron? The electron was discovered as an 'independent' particle in 1897 by the British physicist Joseph John Thomson (1856-1940) after extensive experiments with cathode rays. (J.J.Thomson: 'Cathode Rays', Philosophical Magazine, vol. 44, (1897)). This year, one hundred years after its discovery, there is no total understanding of this particle, although it is part of all matter. To regard the electron as a 'fixed', limited ball with a definite radius, mass and an inner 'mystical' electrical charge, responsible for a so called electrical force effect, does not give a satisfactory deeper understanding of what an electron really is. The wave quantum mechanical description of an electron does neither give a physical, logical understanding of what an electron is. What is then an electron? In the following I shall set forth new theoretical considerations of the subsystem we call an electron. I assume that electrons are dynamical subsystems in the Universe under constant development. Electrons can be considered as Bose-Einstein condensates consisting of unitons situated in the cosmic uniton field. The de Broglie wavelength of a uniton is equal to the extension of the Universe. The present new cosmological dependent theory is based on my quantum cosmology with the main title: Holistic Quantum Cosmology with Decreasing Gravity. (see this). A consequence of this theory is that gravity in the Universe is constantly decreasing. A mechanical/physical explanation of gravity and its decrease, I have explained in another article with the title: Uniton Mechanical Explanation of Gravity (see this). As the Universe expands and gravity decreases, this will cause that physical geometrical extensions of different subsystems, such as f.i. an electron, also expand gradually as the Universe expands. In the following I shall deduct an equation, showing how the extension of an electron varies with the expansion of the Universe. The equation shows the intimate connection between microcosmos and macrocosmos. It allows me also to calculate the mass of the Universe by means of known atomic physical quantities! In other words: the discovered equation shows that an electron grows in extension as the Universe gets older! I shall also show a physical-mechanical connection between what we call respectively 'gravitational' forces and 'electrical' forces. Fundamentally these forces are a result of mechanical pushing effects – of different intensity – caused by the ubiquituous UNITONS, my name for the physical smallest matter/energy quanta in the Universe. This connection between gravity and electricity, which physicists for centuries have tried to find, I believe thus to have discovered, and I shall explain this discovery in the following.
If an electron has a surplus absorption of unitons, this may correspond to the absorption of a photon.
Let us consider two electrons in rest in the cosmic uniton field. According to known physics, it is assumed that two different natural forces are active between the electrons, namely partly so called attracting gravitational forces, partly repulsive electrical forces. The gravitational forces are calculated by Newton's gravitational law, and the electrical forces by Coulomb's electrostatic force law. The mathematical form of these two force laws is completely identical, which in itself is thought-provoking. The electrical force on each electron, however, is 4.16 · 1042 times greater than the gravitational force. According to my quantum cosmological theory, this figure is valid only in our epoch of the evolution of the Universe, and the number, designated N in my theory, is very important to the whole theory. Let us pose the following question: Is it possible that both the electrical and the gravitational forces – and for that matter, all forces – can be related to and explained by mechanical uniton forces? My opinion is yes! I shall motivate my opinion in the following. If the gravitational and electrical forces between two electrons shall be explained with mechanical uniton forces, the sum of uniton forces, corresponding to what we call electrical forces, must be about 1042 times higher than the sum of the uniton forces corresponding to the gravitational force. The magnitude of the gravitational force Fg on an electron is given by Newton's gravitational law: (1) 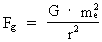 where G is Newton's gravitational 'constant' me the mass of the electron and r the distance between the two electrons in question. The magnitude of the electrostatic force Fe on each electron can be calculated by Coulomb's electrostatic force law: (2) 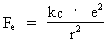 where kc is Coulomb's constant and e is the electric charge of the electron. The ratio between Fe and Fg defines the number N. The ratio between the mass densities of the electron and the Universe.
Let us calculate the ratio between the density of an electron,
(3) 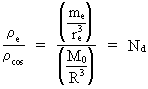 where re is the 'extension' of an electron, M0 is the total mass of the Universe and R its present extension. For the mass and the extension of the universe I use the values I have calculated in my quantum cosmological theory. For the 'extension' of the electron, I use a measured value (re,mes ~ 10-18 m, see f.i. http://www.iop.org/Physics/Electron/Exhibition/section1/ properties.html). The used values are subject to some uncertainty, and this will of cause appear again in the calculated ratio in equation (3). When the known (but uncertain) values are inserted in (3) we get: (4) 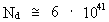
which, as seen, very interestingly is a value near to the number N.
This can not be accidental, there must be a deeper connection!
(5) 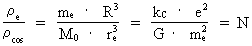
The expression in equation (5) gives us an utterly important and
interesting connection between mostly all the physical quantities, defined
by man in order to describe and understand the Universe, of which we
are ourselves a part. (6) 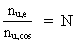 In the following sections, I shall use the connections given by (5) and (6).
Equation (5) gives a connection between the extension of an electron, its mass, electrical charge, Newton's gravitational 'constant', the actual extension of the Universe and its mass. Isolating re we get: (7) 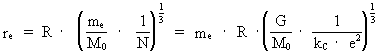 Using the earlier given values for R, M0 and N we get for the extension of the electron: (8) 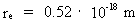
a value very near to the experimental found. Again it must be stressed
that there are uncertainties on the values of R and M0. The
accuracy of these values is determined by the accuracy, by which it is
possible to measure the relative variation of Newton's gravitational
'constant'. "radius of an electron in any direction = a numerical constant times the radius of curvature of space-time in that direction."Equation (7) gives such a context. It should be noted, however, that Eddington before 1929 used the static model of the Universe, which Willem de Sitter (1872-1934) and Einstein worked out, based on Einstein's General Theory of Relativity. Extragalactic systems were for the first time discovered by Edwin Hubble (1889-1953) in 1923. It was also Hubble who discovered the spectral redshift of light from the galaxies in 1929, a phenomenon which has later been interpreted as a universal doppler effect, caused by a general expansion of the Universe. Taking the expansion of the Universe in consideration, as I do, means that the connection between the extension of an electron and cosmological quantities become more complicated than originally imagined by Eddington.
An interesting question is: Is equation (7) also valid for a proton (and maybe
for other so called "elementary particles")? Let us use it on a proton with
the mass mp = 1.67 · 10–27 kg. For the extension
rp we get:
a value near to the measured radius (?) of a proton, which is about 0.86 · 10–15 m, see f.i. under 'Proton' at the URL: http://www.astro.virginia.edu/~eww6n/physics/Proton.html
Instead of expressing the extension of the electron by cosmological quantities, such as the mass of the Universe and its extension, we can on the other hand deduct a connection between the mass of the Universe, M0, and physical quantities, of which the value is well known, maybe just except the extension of the electron. Converting equation (8) gives: (9) 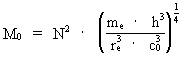 where I have used the following cosmologic basical equation from my holistic quantum cosmology (see this) for the connection between the extension of the Universe, R, and elementary length r0, which on the other hand is determined by Planck's constant, the velocity of light and the mass of the Universe: (10) 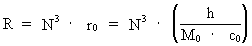 Equation (9) can be written in the following way: (11) 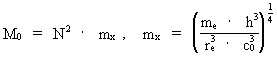 where mx gives the mass of a particle, probably important? As the mass of the Universe is determined by the mass and extension of the electron, it would seem to show that it is the mass of a so called W-particle, which 'appears' at interactive effects, where so called weak nuclear forces are involved. The measured value of the mass of the W-particle is very near to the mass which I have called mx, and is of the magnitude of 10-25 kg, where the mass of the W-particle is measured to about 1.4 · 10-25 kg.
The growing electron. From equation (5) we see that as R, and thereby also G, is changing, some of the other elements in the equation must also change, when the Universe expands. To be in agreement with the assumption I have done in my cosmological theory, f.i. that the mass and electrical charge of an electron are constant, it follows that the extension of an electron will change during time. The equation I deduct shows that electrons increase in extension. In earlier epochs of the development of the Universe their extension was smaller, which of course is quite logical, for how would there otherwise be space for them in a Universe having smaller and smaller volume, when we go back in time? Let us deduct a differential equation for the relative variation of the extension of an electron. Equation (5) can be rewritten as: (12) 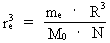 By differentiation of re relative to time (marked by a dot), we get after some calculation: (13) 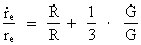
The connection between the relative variation of the extension of the
Universe (14) 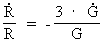 Using this expression in (13) we get: (15) 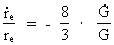
The connection between (16) 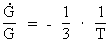 which inserted in (15) gives a connection between the relative variation of the extension of an electron and the actual age of the Universe. We get: (17) 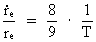 If we wish to get a direct connection between the extension of an electron and the age of the Universe, we can integrate (17) and get: (18) 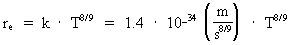 where k is an integration constant. The value of this constant we can determine from the values we know for our epoch. Using values as I have used earlier in this article, we get: (19) 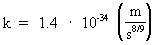 Equation (19) of course is only valid from the 'moment' when electrons were created. The extension of an electron can never have been smaller than elementary length r0 = 10-102 meter. By equation (18) we can calculate the extension of an electron at different ages of the Universe. Let us as an example calculate what the extension of an electron was when the Universe was half a billion years old, viz. when T = 1.6 · 1016 second. From (18) we get: (20) 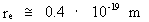 From (20) we see that an electron about 10 billion years ago had an extension about ten times smaller than an electron in our epoch! We can study the processes going on with such electrons by observing very distant objects in the Universe, such as quasars. That the quasars emit very large energies from very small regions can possibly be understood by a.o. the present theory.
By means of the connections found above it can be shown that what we call
'electrical' forces can be related to what we call 'gravitational'
forces. The latter forces can be explained physically-mechanically as
collision forces between unitons. This I have explained in another article.
Electrical forces can thus also be related to uniton pushing forces,
however in a much more intense form. (21) 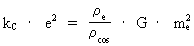
From (21) we see that we can express what we have introduced and called
'electric charge' by purely mechanical and geometrical quantities, namely
mass densities and Newton's gravitational 'constant', which appears as a
coupling parameter. (22) 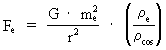
which is a purely mechanical force law. The explanation, why two
electrons repulse each other with forces N times higher than the
forces by which they are pushed together, is that the mass density
of an electron – or the uniton density – is N times higher than the
average overall density of the Universe! The constancy of electrical forces. The expression in (22) gives the magnitude of what we have called the 'electrical' force on an electron, caused by the presence of another electron. You may ask if this 'electrical' force has had the same magnitude, also in earlier epochs of the Universe. If Fe has had the same value through the evolution of the Universe, then the value of the quantity given in equation (23) must be constant through the evolution of the Universe. (23) 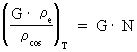 where index T gives the value of the inserted elements at a random cosmical 'moment', later than the moment of creation of electrons. Converting (23) we get: (24) 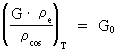 In (24) G0 is the value of Newton's gravitational 'constant' inside the first cosmic time quantum interval of the 'birth' of the Universe. The value of G0 can be calculated very accurately, as it is determined by: (25) 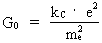
We see that the expression in (23) is constant and equal to G0.
This indicates that the forces active between electrons, and which we
call electric forces, have not changed during the evolution of the
Universe, whereas the gravitational forces are constantly decreasing!
Louis Nielsen, 2nd November 1997.
|
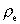 , and the average density of the Universe,
, and the average density of the Universe,
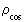 . This is given by:
. This is given by:
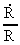 and the relative variation
of Newton's gravitational 'constant'
and the relative variation
of Newton's gravitational 'constant' 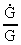 has been
deducted in my cosmological theory, and is given by:
has been
deducted in my cosmological theory, and is given by: