|
The Uniton
– the elementary quantum – building matter,
fields and 'vacuum'
The discovery of a universal quantum ether
By Louis Nielsen, M.Sc., Senior Physics Master
Herlufsholm, Denmark
Introduction
In my holistic quantum cosmology – which can be studied in:
part 1 – I show the existence of a
physically smallest quantum of energy, corresponding to a smallest
physical mass – called elementary mass. This elementary quantum
I shall call a uniton (earlier identified as a graviton). This
name shall show that it represents the smallest energy quantum in the
actual Universe, and furthermore that it is a unity quantum, used to
build matter, fields and the condition called 'vacuum'.
In the following I shall show that what is called vacuum is not an empty
space in the proper sense of this word, but on the contrary 'filled' with
unitons. The existence of this quantum uniton medium is a rediscovery
of the universal ether (from Greek: ,
meaning air), which had already been introduced in archaic time as the
fifth element. (The ether was the 'heavenly' element, the four others
being earth, water, air and fire). This ether medium, which was supposed
to be distributed over the whole Universe, was considered by all
physicists to have a real existence, even if nobody knew what it was
consisting of. ,
meaning air), which had already been introduced in archaic time as the
fifth element. (The ether was the 'heavenly' element, the four others
being earth, water, air and fire). This ether medium, which was supposed
to be distributed over the whole Universe, was considered by all
physicists to have a real existence, even if nobody knew what it was
consisting of.
The ether – also called the light ether – was supposed to be
the medium in which a. o. light travelled. Nobody could in a rational
and physical way understand how for instance light could move from a star
to us, if there were not 'something' to carry it from one point to
another. Several outstanding physicists proposed 'mechanistic' models
for the ether, especially models which were able to explain the
different properties of light. If such a 'mechanical' light ether existed,
it was the belief that it should be possible to show its existence by
interference tests. As the Earth moves around the Sun, the possibility
exists that the ether will cause an 'ether wind'. If the Newtonian laws
for addition of velocities are valid for light, an 'ether wind' would
produce different velocities of light, depending on whether the light
moves in one direction or another, relative to the universal ether, which
in itself defines an absolute frame of reference. According to the
theoretical considerations, light moving in the same direction as the
'ether wind' should have another velocity than light moving in the opposite
direction.
The uniton medium, which I describe, contains so much mass that the
problems with the so-called 'dark matter' and 'missing mass' are hereby
solved. In the following I shall show that if the uniton medium is described
by the ideal gas model, I can, with certain assumptions, calculate that light
phenomena are propagations of uniton oscillations, and that these oscillations
are propagated with the velocity of light. What we call photons must be
identified with 'oscillation quanta' in the uniton medium. By means of this
uniton oscillation model it is possible immediately to understand and reply to
the following question: What happens to a photon when it is absorbed by a
molecule of matter? The answer is: The oscillation energy is transferred
to the molecule, corresponding to the extra oscillation energy which a
light source has transferred to the unitons.
The ether and Michelson-Morley's experiment
The Lorentz transformation
In 1887 a very famous experiment was conducted by Albert Abraham Michelson
(1852-1931) and Edward Morley (1838-1923). (A. Michelson
and E. Morley: "On the 'Relative Motion of the Earth and the
Luminiferous Ether", The American Journal of Science, vol. 34, (1887)).
By this experiment they wanted to demonstrate the possible influence
from the ether on the light. They designed a so-called interferometer,
which should show the possible interference effect of light rays. In the
experiment, a light ray was divided in two, of which the first was forced
to move in the same direction as the Earth moves, the other to move
perpendicular to the first. Having travelled a certain distance, the two
rays met again. If the ether had different effects on the two rays it would
be possible to measure an effect of interference where the two rays met again.
The result was surprising: No interference effect was measured.
There are the following possible explanations to this result:
- The ether moves along with the Earth, thus no 'ether wind' arises.
- The velocity of light – as measured in the chosen frame of
reference – is independent of the movement of the light source relative
to the ether.
- The 'ether matter' passes unhindered through the matter of which the
Earth consists.
- The geometrical conditions of the used device is dependent on the
movement of the device relative to the ether.
- Light does not act as waves in this experiment.
- The ether does not exist.
More explanations are possible, even some which have not been thought out.
One of the explanations accepted eventually by several physicists was a
geometrical effect, even if this is rather strange. In 1889 the Irish
physicist George Fitzgerald (1851-1901) proposed that if bodies were
shortened in the direction of their movements, this might be an explanation
to Michelson's experiment. In 1892 the Dutch physicist Hendrik Antoon
Lorentz (1853-1928) also set forth the thought about a contraction of length.
In H. A. Lorentz: "Versuch einer Theorie der electrischen und optischen
Erscheinungen in bewegten Körpern", Leyden (1895), he showed that
if objects – and this goes for standards, too – are contracted
by the factor: 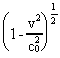 in the direction
of movement, this can explain Michelson's experiment. In this quantity v is
the velocity of the object in the movement direction, relative to the ether,
and c0 is the velocity of light in the ether. Lorentz could give
an electromagnetic explanation of the length contraction. In later theories
Lorentz also introduced coordinate relative time sequences, which led him to
his transformation equations between coordinate systems, moving in relation
to each other with constant speed. Using these transformation equations on
Maxwell's equations will show that these equations are invariant, i. e.
they have the same mathematical form before and after a coordinate
transformation. Albert Einstein (1879-1955) called these transformation
equations for the Lorentz transformation, and he deducted himself the
same equations as Lorentz, however from different basic
principles. These equations are the starting point for Einstein's special
theory of relativity from 1905 (A. Einstein: Annalen der
Physik, vol. 17 (1905)). The initial assumptions are the following: in the direction
of movement, this can explain Michelson's experiment. In this quantity v is
the velocity of the object in the movement direction, relative to the ether,
and c0 is the velocity of light in the ether. Lorentz could give
an electromagnetic explanation of the length contraction. In later theories
Lorentz also introduced coordinate relative time sequences, which led him to
his transformation equations between coordinate systems, moving in relation
to each other with constant speed. Using these transformation equations on
Maxwell's equations will show that these equations are invariant, i. e.
they have the same mathematical form before and after a coordinate
transformation. Albert Einstein (1879-1955) called these transformation
equations for the Lorentz transformation, and he deducted himself the
same equations as Lorentz, however from different basic
principles. These equations are the starting point for Einstein's special
theory of relativity from 1905 (A. Einstein: Annalen der
Physik, vol. 17 (1905)). The initial assumptions are the following:
- All observers, moving relative to each other with constant velocity,
will measure the same value of the velocity of light in 'vacuum', and this
is independent of the movement of the light source.
- The Maxwell equations shall be invariant, relative to a transformation
from one inertial system to another.
By inertial frames are understood frames of reference, moving uniformly
in relation to each other. From the conditions 1) and 2) Lorentz's
transformation equations can be deducted. It shows that the mechanical
Newton laws are not invariant at a Lorentz transformation. Therefore
Einstein redefined the conceptions of distance, time elapse and mass, so
that they had to be understood as relative quantities, dependent on the
movement of the observer. These changes of the basic physical conceptions
led him to a relativistic mechanism, which was also Lorentz invariant.
A consequence – for many physicists dramatical – of Einstein's
special theory of relativity was his claim: there is no universal ether!
The special theory of relativity could explain the result of the
Michelson-Morley experiment. Followers of this theory of relativity were
of the opinion that all speculations about an ether should now cease. But
to throw away an idea which had been part of the natural philosophical
thinking since archaic time was, of course, not easy.
The number of unitons and their distribution in the
Universe
The basis for my holistic quantum cosmology are the quantum cosmological
equations, uniting microcosmos with macrocosmos. The most important
cosmological equation is the following:
(1) 
where R is the actual extension of the Universe, N = 4.16 · 1042
is the ratio between the electrostatic forces and the gravitostatic forces
of an electron and a positron. r0 is the elementary length,
deciding the ratio between Planck's constant and the
total energy/matter mass, M0 of the Universe, multiplied by the
light constant c0.
Equation (1) can be written:
(2) 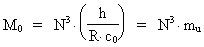
where mu indicates the smallest physical mass in the actual
universe, a mass I have called the elementary mass. This mass corresponds
to a discrete quantum of energy, and is therefore denoted as a uniton.
We see from (2) that the number of unitons is given by
(3) 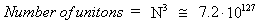
thus a very high number.
An important question is: How is this huge number of unitons distributed in
the Universe? In order to be able to reply to this question, we must first
pose the following extremely fundamental questions: What does 'matter'
consist of? What does a 'field' consist of? And what we call 'vacuum', does
it consist of anything?
The reply to the three last questions must be: Everything consists of
unitons! As the uniton is the physical possibly smallest energy/matter
unit in the Universe, all elementary particles must be built up by unitons.
The following points characterize 'matter', 'fields' and what I shall rather
call 'physical vacuum':
- The density of unitons, viz. number of unitons per volume unit.
- The geometrical distribution of unitons.
- The relative motions of the unitons.
- 'Matter' particles are characterized by a relatively high density of
unitons.
- A 'field' has a relatively lower density.
- And the 'physical vacuum' has the lowest density.
The characteristics of different matter are determined by differences in
the above mentioned. We know that geometric distribution, density and
relative motion are determining the characteristics of matter. As an
example I can mention the following three materials: graphite, diamond and
the carbon-60 molecule. They all consist of carbon atoms, the main
differences are the geometrical constructions. As known these different
carbon structures have widely different properties. Similarly everything
can be built by unitons.
As 'matter' at a higher level consists of electrons, protons and neutrons,
we can calculate how many unitons are 'bound' in the 'matter particles' if
we know the number of 'matter particles' in the Universe. I shall presume
that there are N² 'matter particles' in the Universe. This number is
around 106 times higher than the so-called 'Eddington number',
which should give the number of protons and electrons in the entire Universe.
This number was calculated by the English astro-physicist Arthur Eddington
(1882-1944). (A. S. Eddington: "The Mathematical
Theory of Relativity", Cambridge, (1923)).
I shall assume that the 'bound matter' in the Universe is equivalent to
N² electrons. The number of unitons, necessary to build an electron
is given by:
(4) 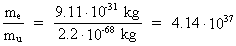
where me is the mass of the electron and mu the mass
of the uniton. We see that the electron is built up by a huge number of
unitons.
The number of unitons bound in 'matter' is given by the number in (4)
multiplied by N². Even if this is an extremely high number, the
difference between the number of 'free' and 'bound' unitons will be around
N³. We can thus presume that there are in average N³ unitons
distributed in the entire Universe, most of them distributed outside the
areas 'occupied' by 'matter particles'. I must thus conclude that what is
called 'vacuum' is absolutely not empty space where nothing exists, but on
the contrary filled with unitons, which have physical existence and physical
effects. I shall therefore name the space between galaxies, stars, atoms and
'elementary particles' as the uniton space. An abstract space
in our mind, where no unitons exist with a physical space of
disposal (Verfügungsraum), gives no physical
meaning.
As evident from the above it seems that I have rediscovered the universal
ether. In my theory, the uniton space is equivalent to the ether. It will
now be a challenge to study the physical effects of the unitons.
Many questions can be posed:
- Does a uniton have an electric charge?
- Is electric charge a mechanical characteristic of unitons?
- Does a uniton have a spin; in the affirmative, how much?
- What is the geometric extension of a uniton?
- How are the motions of a uniton?
- Are all forces the result of collisions between unitons?
- Do gravitational, electromagnetic and other forces propagate through
uniton space?
We can calculate the average occupied volume taken by an uniton. From
equation (1) we can calculate the present total volume of the Universe,
assuming a sphere form:
(5) 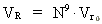
VR is the volume of the Universe with an extension R, and
Vr0 is the volume of a sphere with an extension
equal to elementary length r0. The occupied space of a uniton
Vu is then given by:
(6) 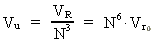
The average extension ru of the occupied space of a uniton is
given by:
(7) 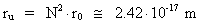
The calculated value of ru is apparently of the same order as
the extension of an electron!
The average uniton density in the Universe is determined by:
(8) 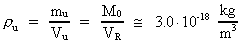
From equations (1) and (7) we get for the ratio between the extension R
of the Universe and the extension of the occupied space of a 'free'
uniton, ru:
(9) 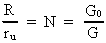
We see that this ratio is equal to the ratio between the electrostatic
and the gravitostatic forces between an electron and a positron, or equal
to the ratio between the gravitational "constant" at the
'birth' of the Universe and the gravitational "constant" of
our epoch.
The mass Ms of the unitons 'bound' in matter I assume given by
the following:
(10) 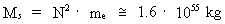
where me is the mass of the electron.
This value is changed if you calculate N from the mass of the proton
instead of the mass of the positron. My choice is done from the physical
philosophical view that I consider the positron to be more fundamental than
the proton. Future observations and experiments must decide which is the
correct choice. The mass in (10) will be 1836² times smaller, and the
average occupied space for a uniton will be 1836 times greater, if N is
calculated, based on the proton mass. The number 1836 is the ratio between
the mass of a proton and the mass of an electron.
Analogy between propagation of sound and propagation
of light in the uniton space
As uniton space with its discrete elementary quanta – the unitons –
is the possible medium through which light and other phenomena, such as
gravity, may travel, I shall shortly explain the mathematical description
of sound waves, i.e. oscillation of particles. The sound effect is an effect
of force caused by particle oscillations. These particle forces can be
transferred from particle to particle and thereby from one position to
another. Necessary for the propagation of a sound wave is that a medium
is present, consisting of 'particles' which can 'convey' a certain
oscillation condition from particle to particle. The speed by which an
oscillation is transferred depends on the special particle medium.
Let us consider the propagation of an oscillation through a row of particles,
situated along a straight line. If the oscillations of the single particles
have the same direction as the direction of the transmission we call it
longitudinal waves. If the single particles oscillate perpendicular to the
direction of the transmission, we call it transversal waves.
Let us introduce an x-axis along the considered row of particles. At rest
or in equilibrium, each particle has an x-coordinate. Let us denote each
particle's displacement from equilibrium with u(x,t). As written, the
displacement is dependent on the coordinate, x, and the time, t, as
measured on a chosen watch. For u(x,t) the following partial differential
equation is valid – permitting a continuous mathematical description:
(11) 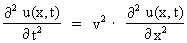
In equation (11) v is the speed of the wave (phase velocity).
The general solution function to the differential equation (11) is given by:
(12) 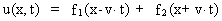
where f1(x-v·t) is indicating a wave travelling in the
positive direction of the x-axis, and f2(x+v·t) a wave
travelling in the opposite direction. The solution (12) thus gives a
superposition solution. Waves travelling through space satisfy the more
general differential equation:
(13) 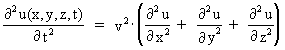
where y and z are directions perpendicular to the x-axis.
The speed of propagation of a given wave is determined by the physical
properties of the wave medium, for example it can be a gas, liquid or
solid matter.
For a gas, where the travelling of a wave is adiabatic, viz. where there
is no exchange of heat between interactive 'volume elements', the
following equation is valid for the velocity, v:
(14) 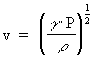
where 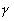 is the ratio between the specific
heat capacity of the gas at constant pressure and constant volume, P is
the gas pressure, and is the ratio between the specific
heat capacity of the gas at constant pressure and constant volume, P is
the gas pressure, and 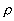 is the mass density
of the gas. is the mass density
of the gas. 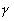 is approximately equal
to 1. is approximately equal
to 1.
If it concerns an ideal gas, viz. an idealized particle system with no
forces between the particles, the following equation of state can be used:
(15) 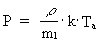
where P is the gas pressure, 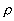 the
mass density of the gas, m1 the mass of the single particle,
Ta the absolute temperature of the gas, and k = 1.38 ·
10-23 J/K is Boltzmann's constant. the
mass density of the gas, m1 the mass of the single particle,
Ta the absolute temperature of the gas, and k = 1.38 ·
10-23 J/K is Boltzmann's constant.
The absolute temperature, Ta, of a gas is defined as
being proportional to the average kinetic energy of a single particle.
If a particle has three degrees of freedom for motion, the following
is defined:
(16) 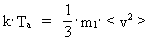
where <v²> is the quadratic mean value of the velocities
of the single particles.
From (15) we get:
(17) 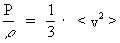
As the uniton is the smallest quantum in the Universe, it is reasonable
to postulate that it moves within its occupied space with an average
velocity of c0, which is the highest velocity in the Universe.
Assuming that light is oscillation transmitted by the uniton space, and
that the equations valid for particle oscillations are also valid for the
unitons, we get for the velocity of transmission of the uniton oscillations,
v, viz. the effects of light:
(18) 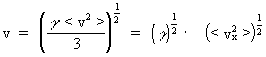
as it is valid that <vx²> = 1/3 · <v²>,
which gives the velocity of transmission along an x-axis. For
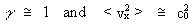 we get: we get:
(19) 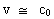
thus a velocity of propagation equal to the speed of light. Travelling of
light from position to position can thus be considered to be propagation
of uniton oscillations. A further knowledge of the conditions of motion
and interaction of unitons will give a better understanding.
From equation (16) we can determine the equivalent absolute temperature
Ta of the uniton space, with a mass of the uniton
m1 = 2.2 · 10-68 kg and <v²> =
c0²:
(20) 
We see that the temperature of the uniton space is very near to absolute
zero. At such low temperature, the uniton medium must have superfluent
properties, a.o. without friction. This freedom of friction means that
all "macroscopic" bodies can move freely through uniton space.
Unitons and their velocities
In my holistic quantum cosmology it is shown that the Universe in
our epoch contains about 10127 matter/energy quanta. They
are created by quantum disintegration of the original cosmic
embryoton - the archaic quantum of which our Universe is created.
I have called these elementary quanta unitons. The present mass
mu of a uniton is in our epoch about 2.2 · 10-68
kg.
The average distribution of the unitons in the Universe corresponds to
an average occupation distance between the unitons of about
10-17 m. See the section about the uniton.
An important question is: By which velocities can unitons move?
Immediate physical logics tells us that, being the smallest
'matter/energy quantum'
in the Universe, it must be able to move at the highest velocity. With
our
present knowledge this velocity is supposed to be the speed of light
in what is called vacuum. It is disputed whether superluminal velocities
exist. Several groups of researchers have conducted experiments
indicating the possibility of superluminal speeds.
In the following I shall show that the minimum velocity of the uniton
is the speed of light c0.
By equations I shall motivate this postulate as follows:
Let us use an equation, first introduced by Louis Victor de Broglie
(1892-1987): Louis de Broglie, Comptes Rendus, vol.177, (1923)):
(21) 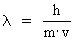
where 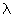 is the
associated 'wavelength' of a particle with the mass m and the
velocity v. h is Planck's constant. is the
associated 'wavelength' of a particle with the mass m and the
velocity v. h is Planck's constant.
We now pose the question: Which is the minimum velocity
vmin
of a uniton, corresponding to the greatest physical 'wavelength'?
The greatest physical distance is the actual extension of the Universe,
R.
The greatest physical 'wavelength' must be equal to R, viz.
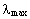 = R.
Using equation (21) we get: = R.
Using equation (21) we get:
(22) 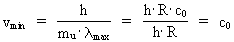
where 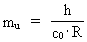 . .
This shows that uniton velocity is equal to the velocity of light.
Lower velocities will correspond to de Broglie 'wavelengths' greater
than the extension of the Universe, and this is physically impossible.
If the above deduction is correct it is evident that a uniton can not
move slower than the velocity of light.
Holism and not separable events
The de Broglie equation and the cosmological basic equation
immediately gives possibilities for uniton
velocities higher than the velocity of light, corresponding to de
Broglie 'wavelengths' smaller than the actual extension of the Universe.
Theoretically the smallest physical 'wavelength' is elementary length.
If we use elementary length in the de Broglie equation we get a
velocity extremely much higher than the velocity of light. A calculation shows
that this maximum velocity is given by: vmax = N3
· c0, where N3 is the cosmic evolution
quantum number.
If a signal moves with this maximum velocity, an event going on in one
end
of the Universe will be able to 'contact' the other end of the Universe
within elementary time!
The possibility of such extreme velocities may give an explanation for
e.g.
Alan Aspect's experiment in 1982 (Physical Review Letters, vol. 49,
(1982)).
Aspect's experiment, and other experiments, show that events happening
so far
from each other that connection by signals travelling by the velocity
of light
is impossible, apparently have almost immediate 'contact' with each
other.
Experiments show that all events in the Universe are connected so, that
an information about an event happening in one subsystem is almost
momentarily 'transmitted' to other subsystems in the Universe. If
actions
can move at superluminal speed and thereby arrange almost momentary
contacts with all other parts of the Universe must be shown by future
experiments and considerations. Theoretically the possibility seems to
exist.
What David Bohm (1917-1992) calls "the enfolded order" and which
quantum physicists in lack of a deeper understanding call "hidden
variables"
can maybe find a physical explanation by my cosmological
uniton theory.
© Louis Nielsen
April 1997 and February 1998 |
Uniton collisions as a physical-mechanical explanation
of gravity and inertia
By Louis Nielsen, Senior Physics Master, Herlufsholm
Since Isaac Newton (1642-1727) around 1660 discovered the
mathematical laws for gravitational forces between two symmetrical,
ball shaped bodies, scientists have tried to find a physical-mechanical
cause for the gravitational effects. Newton himself did not put forward
any hypothesis, able to give a physical explanation of gravity, but he
did not accept that the effects of gravity could be transmitted in an
absolutely empty space and with infinite velocity. This is evident a.o.
from an exchange of letters around 1692-93 with Richard Bentley
(1662-1742), who was curate in London. In his third letter to Bentley,
Newton writes (Isaac Newton's Papers and Letters on Natural Philosophy,
ed. I. B. Cohen, Cambridge, Harvard University Press,1958):
'That gravity should be innate, inherent, and essential to matter, so
that one
body may act upon another at a distance through a vacuum, without the
mediation
of anything else, by and through which their action and force may be
conveyed
from one to another, is to me so great an absurdity, that I believe no
man who
has in philosophical matters a competent faculty of thinking, can ever
fall into
it.'
Newton thus did not accept that gravity could be transmitted through an
empty space without matter. In his opinion there must be a 'medium',
through which the effects of forces are forwarded. Such a universal
'medium' was postulated already in archaic time, when it was called
'ether'. Theories of a universal medium through which also light and
other electromagnetic forces travelled were very common in the last
half of the 19th century.
The ideas about a universal ether were abolished when Albert
Einstein (1879-1955) set forward his Special Theory of Relativity
in 1905. (Annalen der Physik, vol. 17, (1905)). Einstein did not agree
that the existence of a universal 'medium of transport' was necessary,
neither for light, nor for gravity. In 1915, Einstein published his
General Theory of Relativity, which also intended to give an
'explanation' of gravitational phenomena. Einstein explains gravity as
a geometric space-time effect, which is determined by the presence of
matter/energy. In short, the content of Einstein's theory of gravity
is:
- Matter/energy determine space-time geometry.
- Space-time geometry determines the motion of matter.
In Einstein's theory gravitational effects are 'explained' as 'caused'
by 'curved space'. That a space, absolutely empty of matter, can
possess geometric properties, can, however, not be accepted as a
physical explanation! A similar geometric model description was known
from the ptolemaeic theory for the planets motions. This purely
geometric theory could explain many of the observations existing for
the motions of the planets, but, as it is now known, the physical
reality is completely different.
Even if a universal medium is not a consequence of Einstein's
gravitational theory, he could not deny the existence of it.
In my 'Holistic Quantum Cosmology with Decreasing Gravity'
(see this), it is a natural consequence that a
universal 'quantum ether' exists, consisting of extremely small
elementary quanta, which I call unitons (see the beginning of
this article). The unitons move with at least the velocity of light. As
these unitons may be found everywhere in the Universe, thus also in
spaces we call vacuum, it may well be these elementary quanta, which by
thrusting effects are the physical cause of gravity, maybe even
electric forces, other forces and the inertial effects of bodies.
Today most physicists accept Einstein's gravitational theory without
any deeper knowledge of it. We have learnt it in school and at the
university, so it must be right, one says, and is satisfied without
questions.
In the next section I shall shortly mention a mechanical-physical
theory for gravity, developed at the end of the 18th century.
George-Louis Le Sage's mechanical gravitational theory.
Late in the 18th century, the Swiss mathematician and physicist
George-Louis Le Sage (1724-1803) proposed a mechanical
gravitational theory. (George-Louis Le Sage, 'Lucréce
Newtonien', Memoires de l'Académie
Royale des Science et Belles-Lettres de Berlin. Berlin 1784). The
theory has been discussed by a.o. Pierre Prevost (Pierre Prevost,
'Traité de Physique Méchanique de Georges-Louis Le
Sage.' Deux Traités de Physique Méchanique. Geneva,
1818). The theory is based on the following hypothesis:
- The whole Universe is 'filled' with very small particles (Le Sage
called them 'ultramundane corpuscles'), which at great speed move in
all directions.
- When these particles collide with the particles forming matter,
they exert a force on the latter.
- If a body is alone in the space, filled with corpuscles, it will
be influenced equally from all sides, the resulting force then being
zero.
- If two bodies are present in the particle filled space, there will
be a lower density of 'ultramundane' particles between the bodies than
outside the bodies, because they 'shadow' for these. A result of this
inequality in particle density will be that the two bodies are
pushed together.
In an appendix to 'Lucréce Newtonien' Le Sage resumed which properties
the 'ultramundane corpuscles' should have. The following must be
valid:
1. The extension of the corpuscles is very small compared to the
distance between them.
2. Their motions must be linear.
3. Collisions between them must be very rare.
4. The random motions of the corpuscles can be considered to be a
'linear flow' of particles, moving in millions of directions at
constant speed.
The magnitude of the forces, pushing the bodies together, can be
shown to be proportional with the product of the masses of the bodies
and inverse proportional to the square of distance between them, which
is identical to Newton's gravitational law! That the magnitude of the
forces, pushing the bodies together, is proportional to the product of
the masses, requires that the particles of matter, of which a body
consist, are discretely distributed and that there is much empty space
between the particles.
Le Sage's theory had both supporters and opponents. The opposition was
due to the fact that Le Sage's theory was founded on more, partly
independent hypothesis. The theory was not a logical consequence of a
more fundamental physical theory. The kinetic theory for molecules and
the thermodynamic theories were for instance not yet developed, and
this meant that Le Sage's theory was almost forgotten the next hundred
years after its proposal. When the kinetic theory for molecules was
developed at the end of the 19th century, Le Sage's theory was taken up
to renewed analysis by good physicists as James Clerk Maxwell
(1831-1879) (James Clerk Maxwell, 'Atom' Encyclopaedia Britannica, 9th
ed., vol. 3,1890) and William Thomson (Lord Kelvin) (1824-1907)
(William Thomson, 'On the Ultramundane Corpuscles of Le Sage', The
London, Edinburgh and Dublin Philosophical Magazine and Journal of
Science, vol. XLV, London 1873). Physical objections to Le Sage's
theory were a.o. the following: If the planets move through a space,
filled with particles, firstly they will encounter a frictional force,
and secondly their temperature will raise. The problem of friction can
be removed if the 'ultramundane corpuscles' are extremely small and
move at velocities much higher than the speed of the macroscopic
bodies. For the heating problem Lord Kelvin proposed a solution. As in
the kinetic theory for molecules he suggested to operate with three
forms of kinetic energy, viz. translational, rotational and
vibrational. When a 'gravitational particle' transfers impulse to a
body and thereby gets a reduction in f.i. the kinetic energy, this loss
of energy can be compensated for by a possible partial increase of the
rotational and/or the vibrational energy.
Georg Howard Darwin (1845-1912), son of Charles Darwin
(1809-82) and professor in astronomy at Cambridge University, showed
that Le Sage's 'ultramundane corpuscles' have to perform inelastic
collisions with the bodies they collided with, if the exerted forces
shall be able to fulfil Newton's gravitational law. (George H: Darwin,
'The Analogy between Le Sage's Theory of Gravitation and the Repulsion
of Light'., Proceedings of the Royal Society, vol. 76, (1905)).
The Cosmic Uniton Field as Mediator of Force.
One of the problems of Le Sage's gravitational theory was that it
was not a consequence of a more fundamental physical theory. When the
kinetic molecule theory and the thermadynamic theories were developed,
these theories might have formed the mechanical part of the theory.
However, the fundamental assumption, that the whole Universe is
'filled' with 'ultramundane corpuscles', was missing.
This assumption was an ad hoc assumption, which was not a
consequence of for instance a cosmological theory.
In my 'Holistic Quantum Cosmology with Decreasing Gravity', it is a
consequence of the theory that the Universe is filled with the smallest
possible matter/energy quanta, — elementary quanta which I call
unitons. As evident from my quantum cosmological theory, the
Universe started with one quantum, which I call the cosmic
embryoton (the cosmic foster particle). The development of the Universe
is controlled by a cosmic evolution quantum number (the cosmic
quantum clock), which 'ticks' up through all natural numbers!
When the Universe was 'born' it took the value 1! In our epoch, this
cosmic evolution quantum number has reached the extremely high value
of 7·10127.
At every 'tick' of the cosmic evolution quantum number, a new
matter/energy quantum emerges — a new uniton! The number of unitons is,
at every stage of the development of the Universe, equal to the actual
value of the cosmic evolution quantum number — N³. In our
epoch this number is extremely high. Due to the expansion of the
Universe, a decrease in density of unitons takes place, and
simultaneously the mass of each uniton decreases — this is because in
my theory I assume that the total mass of the Universe remains
constant. This dilution of the cosmic uniton field can give a
physical-mechanical explanation of why the gravity in our Universe is
constantly decreasing!
Unitons have extremely small extensions, equal to the elementary
length, and move with the velocity of light (possibly with higher
velocity). All 'matter' is assumed to consist of unitons. Thus f.i. an
electron can be considered to consist of a dynamical subsystem of about
1037 unitons. That an electron is a uniton dynamical system
means that it in a balanced position emits and absorbs the same number
of unitons per unit of time.
As the unitons may be the particles which cause gravitational forces —
and for that matter possibly also other forces — and as these
elementary quanta apparently fulfil the criteria required by Le Sage's
theory, there is a good reason to take this mechanical theory up to
renewed studies, 200 years after it was proposed by the mechanically
intuitive physicist and mathematician George-Louis Le Sage.
Louis Nielsen, 20th October 1997.
E-mail: louis44nielsen@gmail.com
Next article
Main entry
|
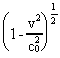 in the direction
of movement, this can explain Michelson's experiment. In this quantity v is
the velocity of the object in the movement direction, relative to the ether,
and c0 is the velocity of light in the ether. Lorentz could give
an electromagnetic explanation of the length contraction. In later theories
Lorentz also introduced coordinate relative time sequences, which led him to
his transformation equations between coordinate systems, moving in relation
to each other with constant speed. Using these transformation equations on
Maxwell's equations will show that these equations are invariant, i. e.
they have the same mathematical form before and after a coordinate
transformation. Albert Einstein (1879-1955) called these transformation
equations for the Lorentz transformation, and he deducted himself the
same equations as Lorentz, however from different basic
principles. These equations are the starting point for Einstein's special
theory of relativity from 1905 (A. Einstein: Annalen der
Physik, vol. 17 (1905)). The initial assumptions are the following:
in the direction
of movement, this can explain Michelson's experiment. In this quantity v is
the velocity of the object in the movement direction, relative to the ether,
and c0 is the velocity of light in the ether. Lorentz could give
an electromagnetic explanation of the length contraction. In later theories
Lorentz also introduced coordinate relative time sequences, which led him to
his transformation equations between coordinate systems, moving in relation
to each other with constant speed. Using these transformation equations on
Maxwell's equations will show that these equations are invariant, i. e.
they have the same mathematical form before and after a coordinate
transformation. Albert Einstein (1879-1955) called these transformation
equations for the Lorentz transformation, and he deducted himself the
same equations as Lorentz, however from different basic
principles. These equations are the starting point for Einstein's special
theory of relativity from 1905 (A. Einstein: Annalen der
Physik, vol. 17 (1905)). The initial assumptions are the following:

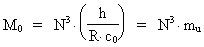
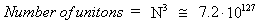
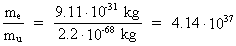
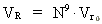
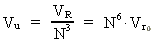
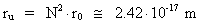
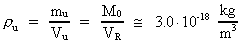
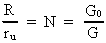
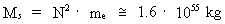
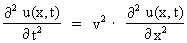
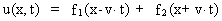
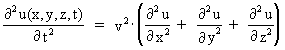
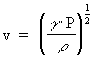
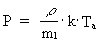
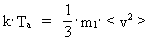
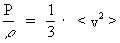
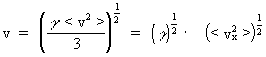
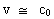

 ,
meaning air), which had already been introduced in archaic time as the
fifth element. (The ether was the 'heavenly' element, the four others
being earth, water, air and fire). This ether medium, which was supposed
to be distributed over the whole Universe, was considered by all
physicists to have a real existence, even if nobody knew what it was
consisting of.
,
meaning air), which had already been introduced in archaic time as the
fifth element. (The ether was the 'heavenly' element, the four others
being earth, water, air and fire). This ether medium, which was supposed
to be distributed over the whole Universe, was considered by all
physicists to have a real existence, even if nobody knew what it was
consisting of.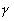 is the ratio between the specific
heat capacity of the gas at constant pressure and constant volume, P is
the gas pressure, and
is the ratio between the specific
heat capacity of the gas at constant pressure and constant volume, P is
the gas pressure, and 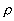 is the mass density
of the gas.
is the mass density
of the gas. 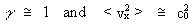 we get:
we get: