Unitondefineret masse
Som Galileo Galilei (1564-1642) viste ved forsøg, falder alle legemer uanset deres masse med samme acceleration i et lufttomt rum. Denne eksperimentelle erkendelse modbeviste Aristoteles' påstand om, at et tungt legeme falder hurtigere end et lettere legeme. I den newtonske mekanik følger det af Newtons 2. lov og Newtons gravitationslov, at legemer med forskellige masser falder med samme acceleration i nærheden en en graviterende masse. Forudsætningen for dette er dog, at et legemes inertielle masse er identisk med dets gravitationelle masse. At disse to masseangivelser der er defineret på tilsyneladende forskellige måder har samme talværdi har givet meget stof til eftertanke, siden Newton opdagede gravitationsloven. Identiteten mellem inertiel masse og gravitationel masse er en af grundforudsætningerne for gyldigheden af Einsteins generelle relativitetsteori fra 1915, hvor den betegnes som 'ækvivalensprincippet'.
En partikels inertielle masse defineres i Newtons 2.lov som forholdet mellem størrelsen af den resulterende kraft på partiklen og størrelsen af den resulterende acceleration. Den gravitationelle masse af en partikel er defineret ved Newtons gravitationslov.
Da alt 'eksisterende' ifølge min holistiske kvantekosmologi antages at bestå af unitoner (se unitonafsnittet) i mindre eller større koncentration vil jeg her give en unitonbaseret definition af masse. Lad os definere: Et systems unitonmasse m er ligefrem proportional med antallet N_u af unitoner i systemet, dvs. der gælder:

(1)

hvor m_u er en proportionalitetsparameter, som kan kaldes masseproportionalitetsparameteren, der vedtages at have enheden kilogram.   m_u er lig med massen af én uniton.

Unitonbestemte gravitationskræfter på to forskellige legemer
I det følgende vises, at legemer med forskellige masser har samme faldacceleration. Jeg benytter min unitonmekaniske gravitationsteori. Grundlaget for denne er min opdagelse (se unitonafsnittet) af eksistensen af et universelt 'kvantemedium' - det kosmiske unitonfelt - bestående af universets aktuelle mindste 'stofkvanter', kaldet unitoner. Disse unitoner er til stede overalt i universet.
Unitoner har en uhyre lille udstrækning og bevæger sig med lysets hastighed (muligvis med endnu større hastighed). Alt 'stof' antages at bestå af unitoner. Således forestilles en elektron at være et dynamisk subsystem bestående af omkring 10³⁷ unitoner. At elektronen er et unitondynamisk system betyder, at den i en ligevægtstilstand emitterer og absorberer lige mange unitoner pr. tidsenhed. Frastødningskraften mellem to elektroner kan meget vel være forårsaget af de unitonstødkræfter, der opstår ved emission- og absorptionsprocesserne (se en anden artikel af mig).

Lad os betragte to legemer 1 og 2 med de forskellige masser m₁ og m₂. Lad først det ene legeme falde i et homogent og konstant gravitationsfelt, og dernæst det andet legeme. I unitongravitationsteorien betyder dette, at unitontætheden (dvs. antal unitoner pr. volumenenhed) uden for legemerne og mellem legeme og det legeme, der faldes mod, er uens men konstante, se figuren. Årsagen til de forskellige unitontætheder er, at legemerne 'skygger' for det kosmiske unitonfelt.

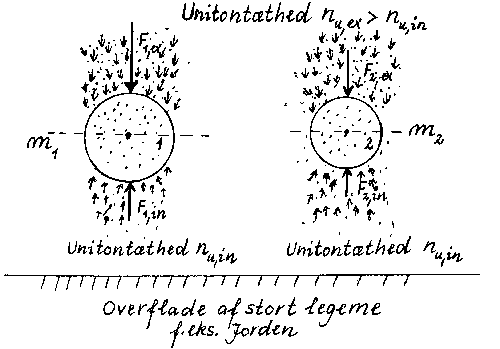
De betragtede legemers masser m₁ og m₂ kan ifølge definitionen i (1) angives som:

(2)

(3)

hvor N_u,1 er antallet af unitoner i legeme 1, og N_u,2 antallet af unitoner i legeme 2.

Lad os overveje de unitonstødkræfter der påvirker legemerne. På legeme 1 virker en extern samlet kraft F_1,ex der må være ligefrem proportional med både den ydre unitontæthed - antal unitoner pr. volumenenhed - n_u,ex (svarende til den kosmiske unitontæthed) og antallet af unitoner N_u,1 i legeme 1.   F_1,ex må således være givet ved:

(4)

hvor k_ex er en proportionalitetskonstant, der karakteriserer det ydre unitonfelt.
For den interne samlede kraft (unitonstødkræfterne på legemets underside) F_1,in gælder analogt:

(5)

hvor n_u,in er den interne unitontæthed, dvs. unitontætheden mellem de legemer, der skubbes sammen.   k_in er en proportionalitetskonstant, der karakteriserer unitonfeltet mellem de to legemer.
Den resulterende kraft F_1,res på legeme 1 er bestemt ved:

(6)

For legeme 2 gælder helt analogt for den resulterende kraft:

(7)

hvor N_u,2 er antallet af unitoner i legeme 2.
Forudsætningen for de lineære kraftudtryk er, at unitontætheden i legemerne er meget små. Dette er også tilfældet, da unitonerne har en uhyre lille udstrækning lig med elementarlængden. Tomrummet udgør således det største volumen af et stoflegeme.

De to legemers accelerationer a₁ og a₂ kan findes ved hjælp af Newtons 2.lov:

(8)

(9)

hvor også den inertielle masse er bestemt efter formel (1).

Da N_u,1 og N_u,2 divideres væk i ligningerne (8) og (9), ser vi, at de to legemer bevæger sig med samme acceleration i overensstemmelse med erfaringerne.

Den gennemsnitlige resulterende stødkraft på en af legemets unitoner F_u er givet ved:

(10)

Hvis der er tale om et frit fald i nærheden af jordens overflade, hvor faldaccelerationen af et legeme er 9,82 m/s² er talværdien af F_u omkring 2 · 10^–67 newton!

Louis Nielsen, 20. okt. 1997
E-Mail: louis44nielsen@gmail.com

  Næste artikel