Forening af Mikrokosmos og Makrokosmos

Universets masse, udstrækning og alder forenet med atomfysiske størrelser

Forening af gravitation og elektricitet

Omnia determinant omnia

Af Louis Nielsen

cand.scient. i fysik og astronomi

Lektor ved Herlufsholm

louis44nielsen@gmail.com

Link til artikler om bl.a. kvantekosmologi:

http://louis.rostra.dk eller http://www.rostra.dk/louis

Forening af Makrofysik og Mikrofysik

Eksisterer der matematisk-fysiske sammenhænge mellem fysiske størrelser, der er karakteristiske for Universet som helhed, og størrelser der er karakteristiske for atomare partikler?

Med andre ord: Eksisterer der sammenhænge mellem naturkonstanter, der er karakteristiske for henholdsvis makrofysik og mikrofysik?

I det følgende vises, at ovenstående spørgsmål, meget muligt, kan besvares med: Ja!

Det vises, at der gælder matematisk-fysiske sammenhænge mellem Universets totale masse, dets udstrækning og kendte naturkonstanter, såsom Newtons gravitationskonstant, Coulombs konstant, lysets hastighed, Plancks konstant og masserne af elektronen og protonen og deres geometriske udstrækninger.

De formulerede formler giver også en forening af elektricitet og gravitation. Det vises, at elektronens og protonens elektriske ladning er bestemt af Universets gennemsnitlige massetæthed. Det vises også at den geometriske udstrækning af både elektronen og protonen afhænger af Universets masse og udstrækning.

Sammenhæng kan næppe være en tilfældighed

Hvis man udregner brøkforholdet mellem middel-massetætheden (dvs. masse pr. rumfangsenhed) af en proton og den gennemsnitlige massetæthed af Universet, så får man et tal uden enhed af størrelsesordenen. Dette tal er så tæt på talværdien, der angiver styrkeforholdet mellem de elektriske kræfter og de gravitationelle kræfter mellem to protoner, at det må antages at der gælder en lighed.

Hvis man udregner brøkforholdet mellem middel-massetætheden af en elektron og den gennemsnitlige massetæthed af Universet, så får man et tal uden enhed af størrelsesordenen. Dette tal er så tæt på talværdien, der angiver styrkeforholdet mellem de elektriske kræfter og de gravitationelle kræfter mellem to elektroner, at man må formode, at det er dette brøkforhold der er tale om.

Ved ovenstående omtrentlige beregninger er følgende talværdier benyttet:

Protonens masse og ’radius’ (omkring værdien af protonens compton-længde). Elektronens masse og ’radius . Universets masse og ’radius’ .

At de nævnte ligheder er tilfældige forekommer usandsynligt. Der må eksistere kosmologiske sammenhænge, sammenhænge vi vil antage og forfølge i det følgende.

Forening af massetæthederne af protonen, elektronen og Universet

Det antages således, at der gælder følgende meget interessante sammenhænge mellem de gennemsnitlige massetætheder af henholdsvis protonen, elektronen og Universet som helhed:

(1)

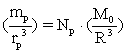
(2)

I ligning (1) er hvilemassen af en proton oger protonens gennemsnitlige ’radius’ (eller ’diameter’).

Protonens middel ’radius’ er med usikkerhed målt til omkring værdien .

I det følgende sættes ’radius’ i anførselstegn, da protonen, elektronen eller Universet som helhed ikke har en fast kugleform.

I ligning (2) er hvilemassen af en elektron og er elektronens gennemsnitlige ’radius’ (eller ’diameter’), der endnu ikke er blevet målt direkte.

er den totale masse af Universet og R dets gennemsnitlige ’radius’.

Styrkeforholdet mellem elektriske kræfter og gravitationelle kræfter

I ligning (1) er lig med styrkeforholdet mellem størrelserne af de elektriske kræfter og de gravitationelle kræftermellem to protoner.

I ligning (2) erlig med styrkeforholdet mellem størrelserne af de elektriske kræfter og de gravitationelle kræftermellem to elektroner.

og er defineret ved følgende:

(3)

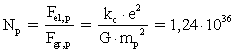
(4)

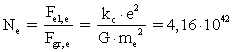
I ligningerne (3) og (4) er Coulombs konstant og er den numeriske elektriske ladning af en elektron eller en proton.

Størrelsener Newtons gravitationskonstant i vor epoke.

Af ligningerne (1) og (2) ser vi, at massetætheden af henholdsvis en proton og en elektron er ligefrem proportional med Universets aktuelle gennemsnitlige massetæthed. Proportionalitetskonstanterne og angiver som nævnt styrkeforholdet mellem de elektriske kræfter og de gravitationelle kræfter mellem henholdsvis to protoner og to elektroner.

Hvad er elektronens ’størrelse’?

I ligning (2) indgår elektronens ’radius’ . Denne er der endnu ikke udført nøjagtige målinger af, men den menes at være af størrelsen , dog med ukendt usikkerhed.

Forklaringen på manglende forsøg til bestemmelse af elektronens ’størrelse’ skal søges i den etablerede Standard Model for ’elementarpartikler’. Denne er en matematisk model, hvor det antages, at elektroner er ’punktformige’ partikler uden geometrisk udstrækning.

Men: Hvis elektroner er reelt eksisterende energi-/stof partikler, da har de naturligvis en reel fysisk, måske oscillerende, geometrisk udstrækning, dette selv om de ikke har en ’fast’ overflade. Så det må være på tide, at udtænke og designe eksperimenter, der ved målinger kan bestemme en elektrons ’størrelse’!

Beregning af Universets masse

Fra ligning (1) kan vi isolere Universets masse :

(5)

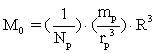
Universets middel ’radius’ R er vurderet til at være af størrelsen . Med denne talværdi for R og fås af ligning (5) for Universets masse:

(5a)

Fra ligning (2) får vi for :

(6)

Benyttes i ligning (6) for elektronens ’radius’ og for Universets ’radius’, da fås for Universets masse:

(6a)

Ligning (6) giver således samme masse af Universet som ligning (5), dog under forudsætning af at de benyttede talværdier for ’radierne’ af protonen og elektronen er korrekte. Det må forsøg eftervise.

Universets ’radius’ koblet med univers-massens compton-længde

Ifølge undertegnedes kvantekosmologi (se link) postuleres følgende sammenhæng at gælde:

(7)

I ligning (7) er Plancks konstant og er lysets hastighed i såkaldt vakuum. Størrelsen i parentesen er lig med den såkaldte compton-længde af massen .

Af ligning (7) kan Universets masse beregnes af:

(8)

Hvis vi i ligning (8) benytter får vi for :

(8a)

Ligning (8) giver, meget interessant, næsten samme talværdi for Universets totale masse som ligning (5) og (6), hvor der indgår både R og protonens og elektronens ’radier’, hvis målte talværdier, som nævnt, er behæftet med usikkerheder.

Fundamentale naturlove der forener mikrokosmos og makrokosmos

Ligningerne (1), (2) og (6) giver næsten ens talværdier for Universets masse. Dette kan ikke være et tilfældigt sammentræf! Ligningerne må således udtrykke nogle fundamentale lovmæssigheder for sammenhængen mellem mikrokosmos og makrokosmos.

Universets ’radius’ og masse beregnet ved hjælp af atomfysiske konstanter

Ved kombination af ligningerne (1), (3), (4) og (7) (og lidt regning) kan Universets ’radius’ R

udtrykkes ved følgende atomfysiske størrelser og gravitationskonstanten:

(9)

Talværdierne af størrelserne i de to første parenteser i ligning (9) er målt med flere decimalers nøjagtighed. Talværdien af protonens ’radius’, placeret i den sidste parentes, er kendt med mindre nøjagtighed.

Hvis vi i ligning (9) benytter får vi for R:

(9a)

Universets masse kan udtrykkes ved følgende:

(10)

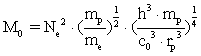
Talværdien af Universets totale masseberegnet af formel (10) giver ikke overraskende:

(10a)

Ligningerne (9) og (10) giver en kosmologisk fundamental sammenhæng mellem Universets ’radius’ R dets totale masse og kendte naturkonstanter, såsom massen af elektronen og dennes elektriske ladning, massen af protonen og dennes radius, Coulombs konstant, Plancks konstant, Newtons gravitationskonstant og lysets hastighed.

I ligning (9) er første parentes ubenævnt. Produktet af de to sidste faktorer i (9) angiver en længde med talværdi , dvs. en masse der er omkring 58 gange protonens masse.

Da de to første faktorer i udtrykket (10) er ubenævnte størrelser (rene tal), så angiver sidste faktor en masse med en talværdi af størrelsen tæt på massen af en proton.

Universets udstrækning

Da R svarer til en tænkt kugles ’radius’, så betyder dette, at Universets aktuelle gennemsnitlige udstrækning er det dobbelte af R.

Den Kosmiske Embryoton. Kvante-længden. Universets kvanteudvikling

Universet begyndte sin dynamiske kvante-udvikling med alt stof og energi koncentreret i en uhyre lille ’partikel’, som vi kan kalde den Kosmiske Embryoton, en betegnelse for den foster-tilstand, hvor alt stof og energi var koncentreret inden for en endelig udstrækning svarende til en fysisk mindste afstand, kvante-længdeneller afstands-atomet, og givet ved:

(11)

Kvante-længden er lig med compton-længden svarende til en masse lig med Universets totale masse .

Universets kvante-udvikling kan tænkes at være foregået ved successive delinger af den oprindelige Kosmiske Embryoton. De dannede stof-/energi-kvanter, som vi kan kalde Unitoner, har siden ved forskellige typer rekombinationer dannet alle de ’partikler’, der eksisterer i det aktuelle Univers.

Det kosmisk embryonale koordinat-system

Den Kosmiske Embryoton kan definere et abstrakt matematisk embryonalt reference-system med et absolut centrum for det udviklende Univers. Positioner og bevægelsesforhold for alle dannede stof-/energi kvanter kan, i princippet, henføres og beregnes i forhold til det embryonale kosmologiske koordinatsystem, som vi kan kalde Det Kosmiske Embryoton-system.

Invariant og absolut hastighed af lyset

Den kosmiske embryotons første kvante-delings proces dannede stof-/energi-kvanter, der bevægede sig af sted med hastigheden, målt i forhold til det kosmiske Embryonale koordinatsystem.

Hastigheden der er lig med den kendte hastighed af lys, er bestemt af brøk-forholdet mellem kvante-længden og et fysisk mindste tidsforløb, tids-kvantet . Dvs. der gælder:

(12)

Da både og er absolutte og invariante størrelser, så gælder dette også hastigheden . Dette er helt i overensstemmelse med målinger af lysets hastighed, der viser, at den er en absolut, ikke-relativ, størrelse.

Forklaringen på den ikke-relative hastighed af lys er således forklaret i ligning (12).

Universets alder

De efterhånden dannede stof-/energi-kvanter har med farten og indtil vor epoke tilbagelagt en strækning lig med Universets nuværende ’radius’ R.

Universets alder T siden dets ’fødsel’ er således af størrelsen:

(13)

Den her, meget simpelt, beregnede værdi af Universets alder er noget lavere end den alder, der (for tiden) regnes med i den etablerede kosmologi.

Hvis protonens ’radius’ er faktoren 1,4 gange større end benyttet, svarende til en proton-radius lig med protonens compton-længde så vil beregningen af Universets alder give 13,8 milliarder år.

Tids-kvantet eller tids-atomet

Ved benyttelse af ligning (7) kan Universets alder T beregnes af følgende ligning:

(14)

’Tids-forløbet’ angiver et mindste fysisk tidsinterval, tids-kvantet eller tidsatomet, givet ved:

(15)

Elektronens ’radius’

Ligning (2) giver en sammenhæng mellem elektronens ’radius’ og Universets masse og dets ’radius’ R.

(16)

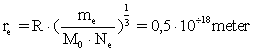
Målinger af elektronens geometriske ’udstrækning’ er som nævnt usikre, men de giver en værdi, der er af størrelsesordenen som teoretisk beregnet i ligning (16).

Sammenhæng mellem elektronens og protonens masser og deres ’radier’

Af ligningerne (1) og (2) og ved benyttelse af (3) og (4) fås følgende simple sammenhæng mellem masserne af henholdsvis elektronen og protonen og deres respektive ’radier’:

(17)

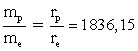
Af ligning (17) ser vi, at elektronens ’radius’ er 1836,15 gange mindre end protonens ’radius’.

Vi får for elektronens ’radius’ :

(18)

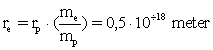
Forening af gravitation og elektricitet

Lovmæssighederne udtrykt i ligningerne (1), (2) og (7) giver en sammenkobling af Newtons gravitationslov og Coulombs kraftlov. Der gælder følgende sammenhæng mellem gravitationskræfterne og de elektriske kræfter mellem to protoner ifølge (1):

(19)

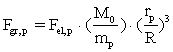
Tilsvarende gælder for sammenhængen mellem gravitationskræfterne og de elektriske kræfter mellem to elektroner ifølge (2):

(20)

Ifølge (7) gælder følgende sammenhæng mellem gravitationskræfterne og de elektriske kræfter mellem to elektroner:

(21)

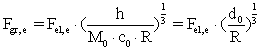
I ligning (21) erkvante-længden givet i ligning (11).

Gravitationskonstantens afhængighed af makrofysiske og mikrofysiske størrelser

Sammenhængene i ligningerne (19) og (20) viser, at talværdien af Newtons gravitationskonstant G afhænger af både kosmologiske størrelser, nemlig Universets totale masse og dets aktuelle ’radius’ og atomfysiske størrelser. Der gælder:

(22)

Svarende til (22) kan G også udtrykkes ved elektronens masse og dennes ’radius’:

(23)

Fra ligning (21) fås et udtryk for G, hvori også Plancks konstant h indgår:

(24)

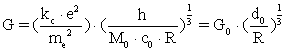
I ligning (24) kan opfattes som talværdien af gravitations-’konstanten’, da Universet kom til eksistens og havde en udstrækning lig med den universelle kvante-længde .

Teoretisk beregning af G ud fra naturkonstanter

Af ligningerne (22), (23) og (24) kan vi teoretisk beregne talværdien af Newtons gravitations-’konstant’ G.

Af ligning (24) får vi med og som forventet:

(24a)

Er elektrisk ladning et mål for massetæthed?

Af de foregående ligninger kan vi udtrykke den elektriske ladning e ved stof-masserne og ’radierne’ af henholdsvis protonen og Universet som helhed:

(25)

Ved løsning af ligning (25) med hensyn til e fås både en positiv og negativ løsning med samme numeriske talværdi::

(26)

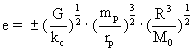
At elektrisk ladning både kan være positiv eller negativ er helt i overensstemmelse med erfaringen.

Vi ser, at e er bestemt af protonens masse og ’radius’ og af den reciprokke værdi af Universets gennemsnitlige massetæthed.

Vi kan også udtrykke e ved elektronens masse og ’radius’. Der gælder følgende:

(27)

Af (26) og (27) ser vi, at elektrisk ladning måske er et mål for mekaniske kraftvirkninger mellem nogle meget fundamentale stofpartikler, dette fordi Universets massetæthed og protonens og elektronens masser og ’radier’ bestemmer størrelsen e.

Protonens og elektronens ’radier’ bestemt ved kosmologiske størrelser

Af ligningerne (22), (23) og (24) kan vi udlede formler, der giver en sammenhæng mellem henholdsvis protonens og elektronens ’radius’ og deres masser og Universets masse og ’radius’.

Vi kan udlede følgende formler for protonens ’radius’ og elektronens ’radius’:

(28)

(29)

Machs Princip

Siden mekanikkens tidligste barndom er der blevet tænkt over de såkaldte fiktive kræfter, også kaldet systemkræfter, idet de giver sig til kende i accelererede systemer. Eksempler på sådanne systemkræfter - der også betegnes inerti-kræfter – er f.eks. centrifugalkræfter og corioliskræfter.

Et spørgsmål, der er blevet stillet: Er disse kræfter fiktive, dvs. 'indbildte' eller er de reelle fysiske kræfter, der forårsages af fysiske systemer? (At kalde dem fiktive, dvs. ’indbildte’ er selvfølgelig helt forkert, da man meget let helt reelt kan blive påvirket af sådanne kræfter, f.eks. ved opbremsning af en bil).

Spørgsmålet er specielt taget op af Isaac Newton (1642-1727), George Berkeley (1685-1753), Ernst Waldfried Josef Wenzel Mach (1838-1916) og Albert Einstein (1879-1955).

Problemstillingen kan illustreres som følger:

Betragt en elastisk deformerbar kugle, der roterer i forhold til resten af Universets stoffordeling. Erfaringen viser, at kuglen vil bule ud ved de ækvatoriale områder. Spørgsmålet er: Hvorfor buler kuglen ud? Newton svarede: Kuglen buler ud, fordi den roterer i forhold til det absolutte rum. Er kuglen i hvile i forhold til det absolutte rum, vil den ikke bule ud, svarede Newton. Den østrigske fysiker og filosof Ernst Mach mente modsat Newton, at der er tale om en relativ effekt, der lige så vel ville opstå, hvis det var hele Universet, der roterede i forhold til kuglen. Newton og Mach var således ikke enige. Ernst Mach analyserede egenskaberne inerti og gravitation, som han redegjorde for i sin bog 'Die Mechanik' fra 1883.

Albert Einstein gik ind for Machs opfattelse og søgte at inkorporere, hvad han kaldte 'Machs Princip' i sin generelle relativitetsteori, men dette er dog ikke lykkedes entydigt.

Machs Princip kan formuleres således:

Inertielle og gravitationelle virkninger er bestemt af den totale stof-fordeling i universet.

Machs Princip opfyldt

I det foregående er der påvist sammenhænge mellem gravitationskonstanten, masserne af protonen, elektronen og Universets samlede masse, altså en sammenhæng mellem gravitationelle virkninger og den totale stofmasse i Universet. Denne sammenhæng opfylder således Machs Princip.

Det Holistiske Princip

Universets totale stofmassedets aktuelle ’radius’ R er de mest fundamentale og mest afgørende fysiske størrelse i Universet. Det er disse størrelser der er primært afgørende for naturkonstanternes størrelse, og dermed naturlovenes virkningsmekanisme. Denne sammenhæng mellem helheden og delen kan vi kalde det ’Det Holistiske Princip’. (Af græsk: Holos: Helhed).

Vi kan formulere mottoet: ’Omnia determinant omnia’. Oversat: ’Alt bestemmer alt’.

Ekspanderer Universet? Evolution af Naturlovene

De foregående formler og sammenhænge kræver ikke nødvendigvis at Universet er under stadig udvidelse. Sammenhængene vil være gældende for et ’stationært’ Univers.

Men: Hvis Universet udvider sig, som målinger tyder på, så bliver Universets ’radius’ R større og større, og dette medfører, at en eller flere af de såkaldte naturkonstanter, f.eks. G, ændrer talværdi (se link). Dette er da ensbetydende med, at Naturlovene ændrer sig og dermed ’deltager’ i en kosmisk evolution.

Da Universet blev ’født’ og var simpelt behøvedes kun ganske få Naturlove. Men efterhånden som Universet blev mere og mere kompliceret, ja da ’udviklede’ der sig flere og flere Naturlove.

(PS.: En analogi med samfundslove: I et samfund med få mennesker og ingen teknik er kun få og simple love nødvendige, mens der i et samfund med mange mennesker og højteknologi kræves flere og mere indviklede love. Lovene udvikler sig med størrelsen af samfundene).

Hvordan kan ovenstående eftervises? Mål ’radierne’ af protonen og elektronen!

Hvordan vil man kunne bekræfte eller modbevise de i denne artikel fremlagte matematisk-fysiske sammenhænge mellem mikrofysik og makrofysik?

Jo, det mest direkte vil være at bekræfte eller afkræfte sammenhængen i ligning (17). Af denne fremgår det, at forholdet mellem protonens ’radius’ og elektronens ’radius’ er lig med forholdet mellem protonens masse og elektronens masse. Dette masseforhold er målt med meget stor nøjagtighed, med en talværdi på omkring 1836.

Så hermed en opfordring til fysikere: Udtænk og design eksperimenter, der kan måle og give nøjagtige bestemmelser af de geometriske ’udstrækninger’ af protonen og elektronen, de to meget almindelige partikler i alt stof!

Louis Nielsen

21/7-2008