|
The quantum energies derived as a consequence of the quantization of space, time and mass By Louis Nielsen, Herlufsholm When Max Planck (1858-1947) about the year 1900 should give an explanation of the curve, showing the distribution of energy of an ’absolutely black body’, radiating energy, he constructed a model for the energy radiating atoms. Max Planck used the following ad hoc assumptions:
With the latter assumption, Max Planck introduced quantum description of phenomenae in nature. According to the classical and mathematically continuous theory for electro magnetism, as expressed by the Maxwell equations, a system can emit or absorb energy in arbitrarily continuous portions. For the classical/mechanical harmonic oscillator (i.e. a particle influenced by an elastic force) is valid that the mechanical energy (viz. the sum of the kinetic and the elastical potential energy) is proportional to the oscillation amplitude to the 2nd power. In continuous classical physics it is also assumed that the energy can take on all continuous positive values, furthermore without an upper maximum value. With the quantum assumption introduced by Planck, a harmonic oscillator can only take on discrete energies En given by: (1) 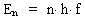 where n is an energy quantum number, which can only take on the values 1, 2, 3, etc. In the traditional wave-quantum mechanics, a relatively complicated mathematical
solution to Schrödinger's continuous wave equation - used on the harmonic oscillator -
gives the values for the energies shown in (1).
Rational quantization of the harmonic oscillator's mechanical energy
The fundamental basis for my ’Holistic quantum cosmology’
(see this) is the quantization of the physically fundamental quantities:
Distance, time interval and mass.
(2) 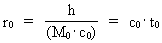 For all phenomenae in our quantized Universe, the following is valid:
(3) 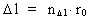 where (4) 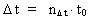 where (5) 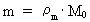 where The transformation from a classical and continuous physical equation to a quantum physical expression is reduced to inserting the quantized quantities given by (3), (4) and (5). Let us quantum transform the equation giving the classical-mechanical energy of a harmonic oscillator. The mechanical energy Emech of a harmonically oscillating particle with the mass m and the amplitude A of the oscillation is, derived according to classical mechanics, given by: (6) 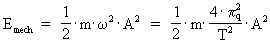 where (7) 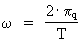 By an index q on (8) 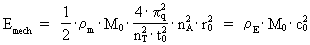 where c0 = r0/t0 is the velocity of light.
By means of (2) we can rewrite (8) to: (9) 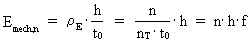 where the rational number Quantized frequency with upper and lower physical limits. The uniton As mentioned the expression in (9) is mathematically identical to (1), however with the great physical difference that the frequency in (9) is quantized, which is a consequence of the quantization of time. In the traditional wave quantum physics, time is not quantized, and thereby derived quantities, such as frequency, are also not quantized. You are also not operating with physical minimum and maximum values of frequency. As the physically smallest time interval is elementary time t0, there must to this correspond a physically highest frequency fmax, given by: (10) 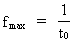 As the greatest time interval is the actual age of the Universe, Tunivers, the physically lowest frequency fmin must be given by: (11) 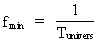 To the physically highest frequency corresponds a maximum energy and a corresponding maximum mass, given by: (12) 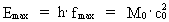 where M0 is the total mass of the Universe and Emax is the
total energy of the Universe.
(13) 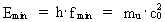
Unification of the smallest with greatest. An interesting question is: Is there a context between the smallest and the greatest physical quantities which describe the Universe? My reply is yes! The reason for my reply can be studied in my 'Holistic quantum cosmology', where I reveal the following contexts: (14) 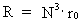 (15) 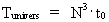 (16) 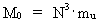
In these equations, N³ appears as a cosmic evolution quantum number,
'ticking' up through the natural numbers. N gives the actual ratio of
the electrostatical and gravitostatical forces between two electrons.
When the Universe was 'born', the cosmic evolution quantum number was equal to
one. (17) 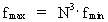 (18) 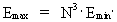 We see that the cosmic evolution quantum number is the physical quantity uniting the smallest and the greatest physical quantities of the Universe.
© Louis Nielsen, December 13th 1998
|
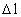 is determined by:
is determined by:
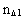 is the space quantum number, which can take on the natural numbers
1, 2, 3, etc.
is the space quantum number, which can take on the natural numbers
1, 2, 3, etc.
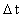 is determined by:
is determined by:
 is the time quantum number, which can take on the natural numbers 1, 2, 3, etc.
is the time quantum number, which can take on the natural numbers 1, 2, 3, etc.
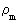 is a rational mass quantum number between 0 and 1.
is a rational mass quantum number between 0 and 1.
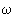 is the angular velocity, which can be calculated by the oscillation time, T, as
follows:
is the angular velocity, which can be calculated by the oscillation time, T, as
follows:
 , I have indicated that
in a physical quantum geometri it is necessary to use a rational pi!
, I have indicated that
in a physical quantum geometri it is necessary to use a rational pi!
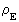 is a rational energy quantum number. Very interestingly we note that the energy content of a specific harmonical oscillator – which is a local subsystem in the Universe – is equal to a rational fraction of the total content of energy of the Universe, which is M0·c0².
is a rational energy quantum number. Very interestingly we note that the energy content of a specific harmonical oscillator – which is a local subsystem in the Universe – is equal to a rational fraction of the total content of energy of the Universe, which is M0·c0².