|
By Louis Nielsen, Senior Physics Master. Introduction. In the following I shall give an alternative derivation of the equations for mass energy and mass increase, and at the same time try to give these equations a physical/mechanical meaning. In 1905 Albert Einstein, in his special theory of relativity, derived an equation telling us that the total energy of a system is equal to the inertial mass of the system multiplied by the velocity of light squared. A deeper physical understanding of this is not available in known physics, and, lacking this, it is assumed that mass energy is a fundamental form of energy, which can not be reduced to anything more fundamental. A consequence of my holistic quantum cosmology is the existence of a smallest matter/energy quantum, which I have called the uniton.The mass energy of a given particle can well be equal to the total kinetic energy of the unitons, of which this particle consists. The equation for mass increase tells us that the inertial mass of a particle increases when its velocity increases. Such equation was in 1905 also derived by Albert Einstein in his special theory of relativity. Experiments conducted by a.o. W.Kaufmann in 1901 and by A.H.Bucherer in 1908: (Bucherer A.H., Verh. deutsch. phys. Ges., vol. 6 (1908)) showed that the inertial mass apparently increases by increasing velocity, in accordance with the following equation: (1) 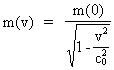
where m(v) is the inertial mass of the particle at the velocity v,
m(0) is the rest mass, viz. the mass at velocity 0, and c0
is the velocity of light in socalled vacuum. In the special theory of relativity it is usual to take the equation for mass increase (1) as a starting point, and from this derive the mass energy equation, or one calculates on a collision between two particles, and then by using the law of conservation of momentum and the transformation equations for velocities from the special theory of relativity, the quantity of mass is redefined thus that it is in accordance with the equation for mass increase, (1). Introducing physical limits on quantities which change with velocity, it is possible to derive the socalled Compton 'wavelength' equation.
In my derivations of the equations for mass energy and mass increase I use Newton's 2nd law, defining the socalled resulting force Fres. Further the definition equation for the work dAres which a force Fres does on a particle over a small distance ds, and the definition of the increase in kinetic energy of the particle, dEk. The following equations are used for calculations in one dimension: (2) 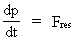 (3) 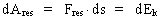 Equation (2) defines the quantity Fres of the resulting force as being the time rate increase of the momentum p of the particle. The momentum of a particle is defined by the product of the immediate inertial mass m(v) - which, as experiments show, is dependent on velocity - and its immediate velocity v, viz.: (4) 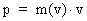 Equation (3) gives the definition of the work done by the resulting force on a particle over the distance ds, and shows that this work defines the increase in the kinetic energy of the particle. In my holistic quantum cosmology I have shown that the total energy, at disposal in the Universe, was 'created' when the Universe did its first cosmic quantum jump over a distance equal to elementary length r0 at about 11 billion years ago. Using equation (3) we can formally calculate the principal maximum work and the associated maximum energy Ecos, which was 'created' at the first cosmic quantum jump. We get: (5) 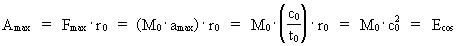 where M0 is the total mass of the Universe and t0 is equal to elementary time. c0/t0 = amax is an upper value for the acceleration and r0/t0 = c0. We see, very interestingly, that the total energy of the Universe is given by the product of its total mass and the velocity of light squared. Thus by an equation identical to the mass energy equation. In my holistic quantum cosmology theory it is assumed that the whole Universe was confined within an extension equal to elementary length when it was 'born'. This state I call the cosmic embryoton. In our epoch the original cosmic embryoton has been broken up in N3 = 7.2 · 10127 matter/energy quanta, called unitons, each with a mass mu = 2.2 · 10-68 kg. The following is valid: (6) 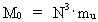 where N is the actual ratio between the electrostatic and the gravitostatic forces between two electrons. Inserting (6) in (5) we get: (7) 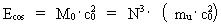 As unitons are the most fundamental physical elements in the Universe and as they do not have an inner structure and are indivisible (the true atoms), the quantity (mu· c0) must be a form of kinetic energy! A form of energy caused by the motion of the uniton. (mu· c02) must be equal to the total kinetic energy of one uniton! All matter - electrons, protons, etc. - and also socalled vacuum, is assumed to consist of unitons, and all effects are assumed to be a result of the motions and collisions of unitons. As for instance an electron consists of 4.14 · 1037 unitons, its mass energy is equal to the total kinetic energy of these unitons! That a system of masses contains energy is thus identical to saying that it consists of unitons with kinetic energy. A particle with the present mass m(v) contains a total energy E, which can be calculated from the equation: (8) 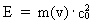 Using equation (4) we can write: (9) 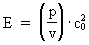 We shall now derive the functional expression for m(v). The expression in equation (3) can be converted to: (10) 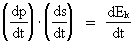
As (11) 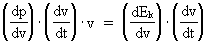 Equation (11) can further be rewritten as: (12) 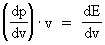 where E = Ek + m0· c02 is the total energy of the particle and m0· c02 is the rest mass energy, which we assume is constant. By differentiation with respect to velocity v, we get from (4) and (8): (13) 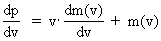 and (14) 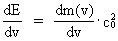 Inserting the expressions from (13) and (14) in (12) we get the following differential equation for determination of m(v): (15) 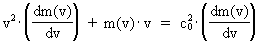 Equation (15) can be rewritten as: (16) 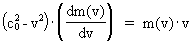 and by separating the variables: (17) 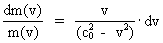 Equation (17) can be integrated as follows: (18) 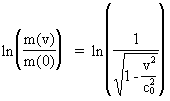 where ln is the natural logaritm. From (18) we get the mass increase equation: (19) 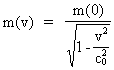 From (19) we see that it is mathematically valid that m(v) goes towards infinity, when v goes towards c0, but physically the mass can not be greater than the total mass of the Universe! I shall revert to this point later. Whether the increase in mass can be explained physical-mechanically or electro-magnetically was discussed much in the beginning of the century. Today physicists assume that this is a fundamental property of matter, which can not be explained by anything more fundamental. However, my uniton theory gives the possibility for an explanation. The following possibilities are imaginable: 1) the increased inertia at higher speeds - corresponding to greater inertial mass - is caused by a 'friction force', arising from collisions with unitons in the cosmic uniton medium, or 2) a particle in motion increases its mass by collecting more and more unitons from the cosmic uniton medium, or 3) it can be 1) and 2) combined. The kinetic energy of a particle Ek can be calculated by: (20)  If c0 is the same for all observers in different inertial systems it will be possible to derive all equations of the special theory of relativity, f.i. the Lorentz transformation equations. According to my theory c0 is given by the ratio between elementary length, r0, and elementary time t0, and as these elementary quantities are invariant for any transformation of coordinates, c0 will also be invariant. An effect which is also a consequence of the special theory of relativity is the socalled length contraction. If a particle (f.i. an electron) has a 'rest extension' l(0) it will, if it moves with a velocity v, get a shorter length l(v) in the direction of its motion, which can be determined by: (21) 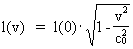 From (21) we see that mathematically l(v) goes towards zero when v goes towards c0, but the physically smallest length which l(v) can get, is equal to elementary length r0!
The mass of a given particle can never physically exceed the total mass of the Universe, M0 and neither can it be smaller than the actual mass of a uniton. Likewise the extension can never exceed the extension of the actual Universe or be smaller than elementary length. If we introduce these limits in the equation for mass increase (19) and the equation for length contraction (21), it is possible to derive the equation for the socalled Compton 'wavelength' of a particle. Let us consider a particle with the rest mass m(0) and the extension at rest l(0), measured in a definite reference system. The principally maximum velocity vmax, by which such particle can move, correspond to a mass equal to the total mass of the Universe, M0 and an extension equal to elementary length, r0. The following must be valid: (22) 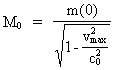
and (23) 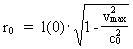 Isolating vmax in (22), respectively (23), we get: (24) 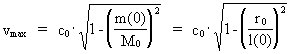
We see from (24) that the velocity of a particle can never reach
c0 exactly. From (24), or directly by multiplying (22) with (23), we get the following connection: (25) 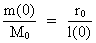 or
(26) 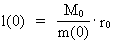 Elementary length r0 has the following connection with Planck's constant h, M0 and c0: (27) 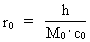 Using (27) in (26) we get: (28) 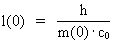 Equation (28) is identical to the socalled Compton 'wavelength equation', except that it has been derived by other means.
It is not quite clear what the distance l(0) reflects concerning the
mass m0. If we use equation (28) on an electron with the
rest mass me = 9.11 · 10-31 kg we get a
Compton length le(0) = 2.43 · 10-12 m.
This distance is not equal to the physical extension of an electron,
which has been measured to be about 10-18 m. According to my uniton dynamical electron model, an electron does not have any definite extension, thus it may be difficult to define it. It corresponds to reply to the question: What is the extension of the atmosphere of the Earth? Equation (28) was first set forward in 1923 together with a report of the socalled Compton effect, when the American physicist Arthur Holly Compton (1892-1962) gave a theoretical explanation of an experimental discovery he had done in 1922. In an experiment X-rays with a definite wavelength were directed towards light atoms, such as carbon atoms. It was shown that the X-rays were scattered in different directions, and that the scattered rays had greater wavelength - and thus lower energy - than the incoming rays. Compton could account for the observed measurements by considering the X-rays as a 'current' of energy rich photons, which at the collisions with the electrons were scattered and thereby lost energy, which was transferred to the electrons. In the uniton theory, the Compton effect may (naively) be explained in the following way: An energy rich photon - consisting of an enormous amount of unitons - collides with an electron, whereby it is divided in two (or more) pieces, and both the electron and the new photons (each consisting of a smaller number of unitons) are scattered in angles, determined in accordance with the laws for conservation of energy and momentum.
© Louis Nielsen, February 1998.
|
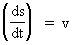 we get:
we get: