Louis Nielsen
Physical Consequences of Decreasing Gravity
Second part of a tretise by Louis Nielsen with new
theory for the evolution of the universe with decreasing
gravity.
Comments by E-mail to:
Louis Nielsen
14. Physical Consequences of Decreasing Gravity
As there is an attracting force of gravity among all particles
of the universe, a decreasing gravity will mean an increasing
distance between them. The consequence is that everything expands!
A constantly decreasing gravity in our universe results in
more physical consequences which are more or less easy to
observe. In the following we shall analyze some of the conditions in the
universe being dependent on the magnitude of gravity.
If we go back to a younger and younger universe, we go to
epochs with higher and higher gravity. But how can we get
knowledge of events which took place billion of years ago?
This we do by observing objects in the sky, farther and farther away. The
informations we get primarily by the light
emitted by the objects, and as this light travels with a
final velocity, we 'see' the condition of the object at the
time when the light was emitted.
Some of the objects presumed to be situated at the greatest
distances, and thus providing the oldest information, are the
so-called quasars. These objects radiate extremely high amounts
of energy from a relatively small geometric area. This is an
actual enigma for the astronomers and physicists. An universal
decreasing gravity may give the explanation.
A geophysical effect of a decreasing gravity is that the globe
is 'inflated', viz. its radius is increasing with time. This
partly causes the surface to crack, and this may explain the
so-called continental or tectonic drift, the phenomenon that
the continents are moving away from each other. Partly it causes the
diameter to grow, causing the rotation to go slower
and slower, and causing the length of the day to increase.
Earlier in the history of the Earth it moved faster. By studying the
continental drift and fossils, proof of decreasing
gravity can be established. The fossils show that certain corals grow a
layer of chalk every day, and observations have
shown that corals millions of years old have thinner and more
layers of chalk than corals from our epoch.
Regarding planetary physics, a decreasing gravity will cause
that the moon moves away from the earth and that all distances
in our solar system increase.
From the formulas it can be calculated that radius of the Earth
increases by about 0.02 cm per year, corresponding to an increase of
radius of about 100 km during the last 500 million years.
This 'inflation' of the earth can explain the forces, which have
been cracking the Earth's crust and split the continents.
As an effect of the decreasing gravity, the distance between the
Earth and the Moon increases by about 1.2 cm per year.
By the increase of the diameter of the Earth, its mass is removed
more and more from the rotation axis, which causes the rotation
speed to decrease (compare with a skater, stretching out his arms
to lower his rotation speed). The slower rotation of the Earth
means that the day is longer. During the last 500 million years
the day has increased by about 1 hour. Another effect, which has
given a further increase in the length of the day, is the tide
effect, the phenomenon giving high and low tide. This is due to
the gravitational pull from both the Moon and the Sun. These
effects cause a slow brake of the Earth.
15. Everything Expands due to Decreasing Gravity
In the following we shall deduct a formula connecting the spacial
expansion of a gravitating system and the relative decrease of the
gravitational 'constant'. We can call it the general expansion
formula.
Let us consider a particle with the gravitational mass m1, moving
in a circular orbit - which shall expand - around another gravitating
particle with the mass m2. The movement of m1 is given by
Newton's 2nd law and the gravitation law, with a gravitational
'constant', having a value at the time of consideration. We get:
(15.1) 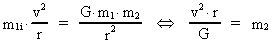
where v is the velocity of m1 and r is the instantaneous distance
between m1 and m2. m1i gives the
inertial mass of the orbiting
particle. We shall consider velocities relatively small to the
velocity of light and shall therefore consider that the inertial
mass is equal to the gravitational mass, m1i = m1.
Let a dot over a letter mean differentiation regarding time (Newton's
notation), and we get from (15.1):
(15.2) 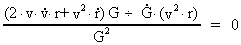
This we can reduce to:
(15.3) 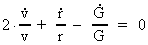
We are handling a central force and there is preservation of
angular moment, thus:
(15.4) 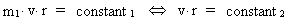
From equation (15.4) we get:
(15.5) 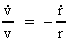
Inserting in (15.3) we get for the relative increase of r:
(15.6) 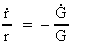
The Expansion Formula
For the relative variation of the velocity we get:
(15.7) 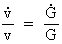
Equation (15.6) shows the radial velocity, whereby two gravitating masses,
spaced by the distance r, will move away from
each other. The relation is a theoretical deduction of the
cosmological Hubble relation!
We shall use (15.6) to calculate the timely increase of the
radius of the Earth and the increase in distance to the Moon,
presuming that:
(15.8) 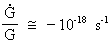
and that this value is nearly constant in our epoch.
For the increase of the radius of the Earth we get (r = 6400 km):
(15.9) 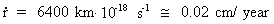
If we use equation (15.6) on the Earth - Moon system, we calculate
a timely increase in distance (r = 384.4 · 103 km):
(15.10) 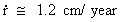
Laser measurements have shown that the distance to the Moon has
increased by about 5 cm/year. The result in (15.10) only gives the
amount due to decreasing gravity. The rest is due to other gravitational
effects, a.o. the tide forces.
Paleomagnetic analyses *) have estimated an upper limit of
0.13 mm/year for the increase in the Earth's radius, in good
agreement with the figure in equation (15.9). The value in (15.9)
is dependent on the precision of the measurement of
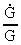
----------
*) Ref.: McElhinny et al. Nature, 271, 316-321 (1978).
16. The Expansion of the Earth and the Increase of the Day
Continental Drift
Eventually, when gravity decreases, the Earth - and all other
globes - will 'inflate', with the result that the mass is
distributed farther and farther from the rotation axis. This
causes the rotation velocity to decrease. A lower rotation
speed is equal to a longer day. The Earth is slowly braked.
Technically speaking, the inertial moment of the Earth increases gradually
as the radius increases.
In the following I shall deduct a formula giving a relation
between the rotation time tr of the Earth at a certain time
and the gravity 'constant' at the same time. As the value of
the gravity 'constant' depends on the age of the universe, a
direct connection to this is also given.
The angular momentum Lj of the Earth can be expressed by its
inertial moment in relation to the rotation axis and the angle
velocity, thus:
(16.1) 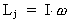
where I is the inertial moment and
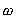 the
angle velocity. the
angle velocity.
Presuming that the angular momentum is constant during 'inflation', we
have:
(16.2) 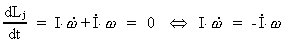
The inertial moment of a ball is:
(16.3) 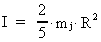
where mj is the mass of the Earth and R the present radius.
If we differenciate I in relation to time, we get:
(16.4) 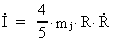
As we have:
(16.5) 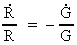
we get from (16.4) and (16.5):
(16.6) 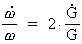
This equation is integrated and if t1 and t2 are two times,
where t2 > t1, we get:
(16.7) 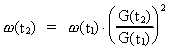
The relation between 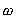 and the rotation time and the rotation time
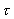 is
given by: is
given by:
(16.8) 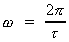
and we get:
(16.9) 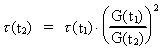
The actual value of the gravity 'constant' depends on the
actual age of the universe:
(16.10) 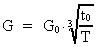
where G0 is the initial gravity 'constant' and t0 elementary time.
Using this in (16.9) we get:
(16.11) 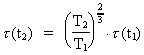
This formula we could also have deducted directly from the
condition of preservation of angular momentum. We shall calculate some
examples. Firstly, we shall calculate the rotation time
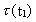 for the
Earth in the Devon period, about 400
million years ago. Using the values T2 = 10.5 · 109 years;
T1 = 10.1 · 109 years, for the
Earth in the Devon period, about 400
million years ago. Using the values T2 = 10.5 · 109 years;
T1 = 10.1 · 109 years,
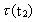 = 24 h, we get: = 24 h, we get:
(16.12) 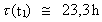
Some scientists have analyzed the relative timely decrease of
the angle velocity of the Earth. The observed value has been
given to:
(16.13) 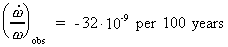
A relatively great amount is due to the gravitational tidal
effects, mainly from the Sun and the Moon. This value amounts
to:
(16.14) 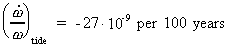
and thus not enough to explain the observed value!
To this, however, comes a contribution from the decreasing
gravity. From equation (16.11) we get:
(16.15) 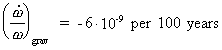
Combining (16.14) and (16.15) we get:
(16.16) 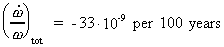
which is in good conformity with the observed value.
17. Decreasing Gravity and Mass-Luminosity of Stars
The radiation of energy from a star (or a galaxy) is known
to be dependent on the mass of the star m, and the gravitational
'constant', G. It can be shown that there is the following connection
between the radiated effect P and m and G.
This relation is normally called the mass-luminosity relation:
(17.1) 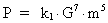
k1 is a system dependent proportionality constant. The
relation is independent of specific energy producing processes.
Let us calculate the relation between energy radiation at
two different times, with two different values of the gravitational
'constant', i.e. two different times T1 and T2
in the age of the universe. We can write:
(17.2) 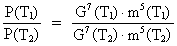
If the mass is presumed to be the same at the two times
we have m(T2) = m(T1) and:
(17.3) 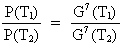
Inserting the expression for the decrease of G relative to
the age of the universe, we get:
(17.4) 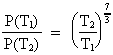
From this equation we see that the radiation of energy from
an object far away from us, for instance a quasar, will be
much stronger, as the light from this object was sent off
at a time when the gravitational 'constant' was greater,
corresponding to a younger age of the universe.
As an example we can use: T1 = 0.5 · 109 years and
T2 = 10.5 · 109 years, which gives:
(17.5) 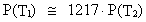
It also follows that the extension of the distribution of
mass is dependent on G, with higher concentration within
a smaller space area in earlier epochs.
The following relation is valid:
(17.6) 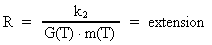
For the two ages we get:
(17.7) 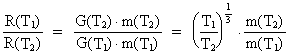
With the ages as above we get:
(17.8) 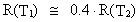
If we in the equations (17.4) and (17.7) use the values
T1 = 106 years and T2 = 10.5 ·
109 years, we get for
respectively radiation of energy and the extension of the
object (T1 is age of the universe):
(17.9) 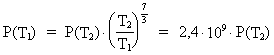
(17.10) 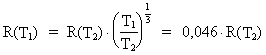
We see from the expressions (17.9) and (17.10) that the farther
away and thus the younger objects we observe, the stronger
radiation and the smaller extension these objects have.
This is exactly what has been observed for the so-called
quasars, namely that they have extremely strong radiations
from relatively small regions. The quasars are known to
be situated in the outermost regions of our universe, i.e.
we observe objects in the young universe. The above given
explanation thus may be the answer to the quasar enigma.
Newer photographs with long exposure times have shown that
the quasar proper apparently is only the central region -
the core - of a very distant galaxy, similar to the so-called N-galaxies
(N for nucleus), situated nearer to us, and
the so-called Seyfert-galaxies, which are still nearer.
The three types of galaxies, S, N and Q-galaxies, may be
proof of a cosmic decreasing gravity.
By the expressions in (17.1) and (17.6) we can calculate the relative
variation in time of P and R. We get:
(17.11) 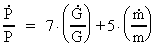
and
(17.12) 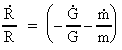
As 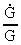 and
and 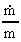 are functions
decreasing in time it will be seen that are functions
decreasing in time it will be seen that
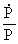 decreases with
time and decreases with
time and 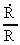 increases
with time. increases
with time.
Post scriptum:
The present theory gives a solution to the 'mystery of large numbers', as
N plays the role as a cosmic evolution parameter, the
value of which was 1 at the birth of the universe.
The theory is compatible with Mach's principle, uniting macro- and
microcosmos.
The theory also answers to 'the arrow of time', as time can only
increase. This is fulfilled by the cosmic space quantum number
and the cosmic time quantum number being integers, moving from 1
to higher and higher values.
18. Centrifugal and Coriolis Forces are identical to the
N¯ Field
Since the childhood of mechanics a great interest has been shown
the so called 'fictive forces' appearing in accelerated systems.
Examples are centrifugal and Coriolis forces. The question is:
are these forces really fictive, or are they real physical forces, caused
by other physical phenomena? This question was especially taken up by
Isaac Newton (1642-1727), George Berkeley (1685-1753), Ernst Mach
(1838-1916) and Albert Einstein (1879-1955).
The problem can be illustrated as follows.
Consider a ball rotating relatively to all other masses of the universe.
Experience shows that the ball bulges at the equatorial
regions. Why is that? Newton said: the ball bulges because it
rotates in relation to absolute space. If the ball were at rest
it would not bulge. On the contrary, Mach said that it is a relative
effect which would also occur if the whole universe rotated
and the ball were at rest. Newton and Mach thus did not agree.
Einstein adopted Mach's viewpoint - everything is relative - and
tried to incorporate Mach's principle in his theories of relativity.
Mach's principle can be formulated:
The local physical effects are relatively dependent on the condition of
the rest of the universe.
I agree with Mach in his opinion, formulating generally: Everything is
dependent on everything. Omnia determinant omnia.
In the following we shall examine the identity of the N Vector
field
( ) and the centrifugal and Coriolis forces. ) and the centrifugal and Coriolis forces.
Consider a particle with the gravitational mass mg in an inertial
system. Let it rotate in a circular orbit with radius vector
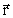 and angular velocity and angular velocity
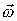 .
The centrifugal force will then be: .
The centrifugal force will then be:
(18.1) 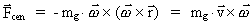
The mathematical form is exactly identical to the expression for
the gravitational  field in equation (9.6): field in equation (9.6):
(18.2) 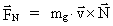
 is the velocity of the gravitational mass in the is the velocity of the gravitational mass in the
 field. The size and direction of this field is thus identical to
field. The size and direction of this field is thus identical to
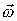 . .
Relatively seen, the total masses of the universe are rotating
in opposite direction of the rotating particle. This will induce
an  field in the area where the particle rotates.
The
exact formula for calculation of the size of field in the area where the particle rotates.
The
exact formula for calculation of the size of
 depends on
the geometric distribution of masses around the rotating particle. If we
consider an depends on
the geometric distribution of masses around the rotating particle. If we
consider an  field induced by a mass
Mg,
distributed evenly in a ring with radius R, we get: field induced by a mass
Mg,
distributed evenly in a ring with radius R, we get:
(18.3) 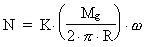 (from equation 9.4)
(from equation 9.4)
where K is the dynamic coupling constant to the
 field. field.
Setting N = 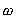 , we get: , we get:
(18.4) 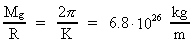
A finer analysis, taking into account the final velocity of
distribution of the field, the variation of K and an exact
geometry, will confirm the above.
19. Inertia. A Measure for Effects of Gravitational Forces
A particle will 'show' inertia (slowness, resistance) against
changes to its velocity in relation to an inertial system,
i.e. against acceleration. This property was introduced in
Newton's 2nd law as inertial mass, mi. mi is the
proportionality factor
between the acceleration and the resulting
force on the particle. Thus Newton's 2nd law:
(19.1) 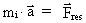
where 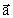 is the acceleration
and is the acceleration
and 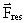 the resulting
force. The question is: what causes this inertia, working
as a force opposite to the force by which the particle is
influenced? A tempting answer is that we have a gravitational
self-inductance, caused by the relative movement in comparison with the
other masses of the universe. If the above
is true, Newton's 2nd law must be changed to a tensor law.
The inertial mass is then not a scalar, but a tensor, which
we can call the inertial mass tensor. The generalised 2nd
law will then be:
the resulting
force. The question is: what causes this inertia, working
as a force opposite to the force by which the particle is
influenced? A tempting answer is that we have a gravitational
self-inductance, caused by the relative movement in comparison with the
other masses of the universe. If the above
is true, Newton's 2nd law must be changed to a tensor law.
The inertial mass is then not a scalar, but a tensor, which
we can call the inertial mass tensor. The generalised 2nd
law will then be:
(19.2) 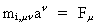
where
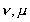 take on all
space coordinates and summation is done over take on all
space coordinates and summation is done over
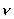 . As the universal distribution of
mass around a particle orbit most likely will be assymmetric, the inertial
mass will be anisotropic. Confirmation of the above must be
done by measuring the inertial mass of a particle as it moves
in different directions. Please note that the gravitational
mass of a particle must be considered invariant. . As the universal distribution of
mass around a particle orbit most likely will be assymmetric, the inertial
mass will be anisotropic. Confirmation of the above must be
done by measuring the inertial mass of a particle as it moves
in different directions. Please note that the gravitational
mass of a particle must be considered invariant.
Louis Nielsen
Mejerivej 25 A
DK-4700 Næstved
Denmark
Comments by E-mail may be sent to:
Louis Nielsen
Next article
Main entry
A good dictionary of computer abbreviations and acronyms with 9.100
entries and 15.000 definitions has appeared in Denmark. It will be very
useful, also to English speaking people, as more than 90 percent of
computer terms are in English.
Gads Lommelex: edb-forkortelser
by Hans Christophersen
G. E. C. Gads Forlag, Copenhagen.
ISBN 87-12-02474-0
Review in Danish or
in German.
| 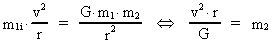
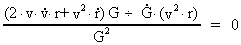
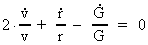
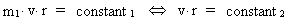
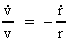
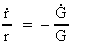
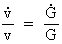
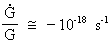
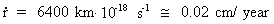
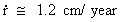
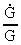
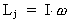
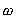 the
angle velocity.
the
angle velocity. 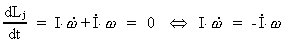
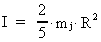
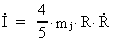
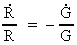
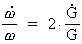
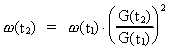
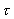 is
given by:
is
given by:
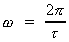
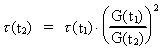
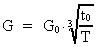
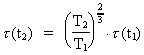
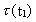 for the
Earth in the Devon period, about 400
million years ago. Using the values T2 = 10.5 · 109 years;
T1 = 10.1 · 109 years,
for the
Earth in the Devon period, about 400
million years ago. Using the values T2 = 10.5 · 109 years;
T1 = 10.1 · 109 years,
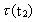 = 24 h, we get:
= 24 h, we get:
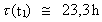
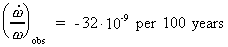
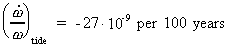
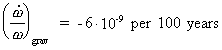
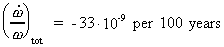
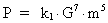
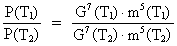
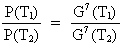
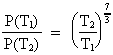
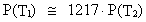
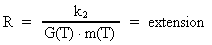
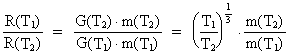
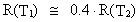
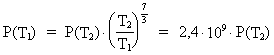
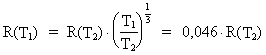
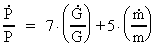
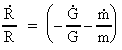
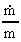 are functions
decreasing in time it will be seen that
are functions
decreasing in time it will be seen that
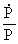 decreases with
time and
decreases with
time and 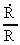 increases
with time.
increases
with time.
 ) and the centrifugal and Coriolis forces.
) and the centrifugal and Coriolis forces.
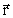 and angular velocity
and angular velocity
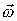 .
The centrifugal force will then be:
.
The centrifugal force will then be:
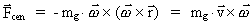
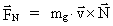
 is the velocity of the gravitational mass in the
is the velocity of the gravitational mass in the
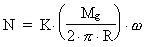
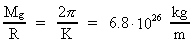
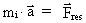
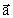 is the acceleration
and
is the acceleration
and 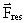 the resulting
force. The question is: what causes this inertia, working
as a force opposite to the force by which the particle is
influenced? A tempting answer is that we have a gravitational
self-inductance, caused by the relative movement in comparison with the
other masses of the universe. If the above
is true, Newton's 2nd law must be changed to a tensor law.
The inertial mass is then not a scalar, but a tensor, which
we can call the inertial mass tensor. The generalised 2nd
law will then be:
the resulting
force. The question is: what causes this inertia, working
as a force opposite to the force by which the particle is
influenced? A tempting answer is that we have a gravitational
self-inductance, caused by the relative movement in comparison with the
other masses of the universe. If the above
is true, Newton's 2nd law must be changed to a tensor law.
The inertial mass is then not a scalar, but a tensor, which
we can call the inertial mass tensor. The generalised 2nd
law will then be:
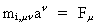
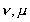 take on all
space coordinates and summation is done over
take on all
space coordinates and summation is done over
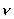 . As the universal distribution of
mass around a particle orbit most likely will be assymmetric, the inertial
mass will be anisotropic. Confirmation of the above must be
done by measuring the inertial mass of a particle as it moves
in different directions. Please note that the gravitational
mass of a particle must be considered invariant.
. As the universal distribution of
mass around a particle orbit most likely will be assymmetric, the inertial
mass will be anisotropic. Confirmation of the above must be
done by measuring the inertial mass of a particle as it moves
in different directions. Please note that the gravitational
mass of a particle must be considered invariant.